Ce chapitre est une présentation des travaux [39, 20, 25, 26, 30, 32].
 Dans ce chapitre, on utilise différents algorithmes de descente de gradient pour plusieurs problèmes d'optimisation. La première section est une présentation des algorithmes stochastiques utilisés dans les sections suivantes. On applique ensuite ces méthodes pour déterminer des courbes médianes, faire de la classification non hiérarchique et pour minimiser un indicateur de risque.
Dans ce chapitre, on utilise différents algorithmes de descente de gradient pour plusieurs problèmes d'optimisation. La première section est une présentation des algorithmes stochastiques utilisés dans les sections suivantes. On applique ensuite ces méthodes pour déterminer des courbes médianes, faire de la classification non hiérarchique et pour minimiser un indicateur de risque.
 On recherche un zéro d'une fonction $f$ à valeurs réelles. On suppose disposer d'une valeur très approximative $x_0$ de cette racine. L'idée naturelle de l'algorithme de Newton est de remplacer la courbe représentative de la fonction $f$ par sa tangente au point $x_n$. L'abscisse $x_{n+1}$ du point d'intersection de cette tangente avec l'axe des abscisses est alors donnée pour $n\geq 1$ par
\[x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}.\]
Sous des hypothèses sur la nature du point fixe de la fonction $x\mapsto x-\frac{f(x)}{f'(x)}$ on obtient la convergence et la vitesse de l'algorithme. Lorsque la dérivée de $f$ n'est pas facilement calculable, on peut considérer une version déterministe de l'algorithme de Robbins-Monro qui consiste à remplacer le calcul de la dérivée par une suite positive décroissante tendant vers $0$ de pas $(\gamma_n)$ telle que la série $\sum \gamma_n$ diverge. A condition que $f$ ait de bonnes propriétés de régularité et convexité (voir par exemple [104]), la suite définie par
\[x_{n+1}=x_n-\gamma_nf(x_n)\]
converge vers le zéro de la fonction $f$, noté $x^*$, pour toute valeur initiale $x_0$.
On recherche un zéro d'une fonction $f$ à valeurs réelles. On suppose disposer d'une valeur très approximative $x_0$ de cette racine. L'idée naturelle de l'algorithme de Newton est de remplacer la courbe représentative de la fonction $f$ par sa tangente au point $x_n$. L'abscisse $x_{n+1}$ du point d'intersection de cette tangente avec l'axe des abscisses est alors donnée pour $n\geq 1$ par
\[x_{n+1}=x_n-\frac{f(x_n)}{f'(x_n)}.\]
Sous des hypothèses sur la nature du point fixe de la fonction $x\mapsto x-\frac{f(x)}{f'(x)}$ on obtient la convergence et la vitesse de l'algorithme. Lorsque la dérivée de $f$ n'est pas facilement calculable, on peut considérer une version déterministe de l'algorithme de Robbins-Monro qui consiste à remplacer le calcul de la dérivée par une suite positive décroissante tendant vers $0$ de pas $(\gamma_n)$ telle que la série $\sum \gamma_n$ diverge. A condition que $f$ ait de bonnes propriétés de régularité et convexité (voir par exemple [104]), la suite définie par
\[x_{n+1}=x_n-\gamma_nf(x_n)\]
converge vers le zéro de la fonction $f$, noté $x^*$, pour toute valeur initiale $x_0$.
 Pour calculer un minimum ou un zéro de fonction, on emploie en général des algorithmes déterministes. Cependant, lorsque la fonction a de nombreux minima proches les uns des autres, ces algorithmes risquent de rester piégés dans des minima locaux. De plus, très souvent dans la modélisation stochastique, la fonction $f$ n'est connue qu'à une perturbation près. On suppose donc que $f$ est de la forme $f(x)=\E[F(x,\xi)]$, où $\xi$ est une variable aléatoire. L'évaluation de la fonction $f$ ne peut être faite que par des mesures approchées. L'algorithme de [121] consiste à remplacer à chaque étape la valeur inconnue $f(X_n)$ par son observation bruitée $Y_{n+1}=F(X_n,\xi_{n+1})$ où les variables aléatoires $\xi_1, \ldots, \xi_N$ sont des différences de martingales. On a en particulier $\E\left[Y_{n+1}|\CF_n\right]=f(X_n)$. L'algorithme de Robbins-Monro est donc défini par
Pour calculer un minimum ou un zéro de fonction, on emploie en général des algorithmes déterministes. Cependant, lorsque la fonction a de nombreux minima proches les uns des autres, ces algorithmes risquent de rester piégés dans des minima locaux. De plus, très souvent dans la modélisation stochastique, la fonction $f$ n'est connue qu'à une perturbation près. On suppose donc que $f$ est de la forme $f(x)=\E[F(x,\xi)]$, où $\xi$ est une variable aléatoire. L'évaluation de la fonction $f$ ne peut être faite que par des mesures approchées. L'algorithme de [121] consiste à remplacer à chaque étape la valeur inconnue $f(X_n)$ par son observation bruitée $Y_{n+1}=F(X_n,\xi_{n+1})$ où les variables aléatoires $\xi_1, \ldots, \xi_N$ sont des différences de martingales. On a en particulier $\E\left[Y_{n+1}|\CF_n\right]=f(X_n)$. L'algorithme de Robbins-Monro est donc défini par
- un cadre réel ou multidimensionnel $\Rset^d$ pour les variables $(Y_n)$,
- une suite de pas $(\gamma_n)$ ni « trop grande » ni « trop petite »,
- un comportement « raisonnable » de la fonction $f$ près du point,
- un comportement « raisonnable » à l'infini.
 En pratique, l'algorithme de Robbins-Monro est très sensible aux paramètres comme le point de départ $X_0$ ou la calibration de la suite de pas $(\gamma_n)$. La vitesse optimale de l'algorithme est atteinte pour un pas de la forme $\gamma_n= c/n$ mais le choix de la constante $c$ est extrêmement important et la déterminer en pratique s'avère très délicat (voir par exemple [104] (Th. 2.2.12)). Pour contourner ce choix critique, [117] proposent une version «moyennisée» de cet algorithme en prenant la suite de pas $(\gamma_n)$ à décroissance plus lente que la vitesse «optimale», par exemple $\gamma_n = n^{-3/4}$. Avec ce choix, les oscillations de l'algorithme $(X_n)$ sont très fortes. Ils lissent alors cette suite d'estimateurs en considérant le «moyennisé» : $\frac{1}{n}\sum_{k=1}^n X_k.$ Sous de bonnes conditions sur $f$, on peut montrer que la convergence est encore vraie et que la normalité asymptotique est également vérifiée, avec la variance optimale, au sens où l'on atteint la covariance de l'algorithme statique. En pratique, cet algorithme est beaucoup moins sensible au choix des paramètres.
En pratique, l'algorithme de Robbins-Monro est très sensible aux paramètres comme le point de départ $X_0$ ou la calibration de la suite de pas $(\gamma_n)$. La vitesse optimale de l'algorithme est atteinte pour un pas de la forme $\gamma_n= c/n$ mais le choix de la constante $c$ est extrêmement important et la déterminer en pratique s'avère très délicat (voir par exemple [104] (Th. 2.2.12)). Pour contourner ce choix critique, [117] proposent une version «moyennisée» de cet algorithme en prenant la suite de pas $(\gamma_n)$ à décroissance plus lente que la vitesse «optimale», par exemple $\gamma_n = n^{-3/4}$. Avec ce choix, les oscillations de l'algorithme $(X_n)$ sont très fortes. Ils lissent alors cette suite d'estimateurs en considérant le «moyennisé» : $\frac{1}{n}\sum_{k=1}^n X_k.$ Sous de bonnes conditions sur $f$, on peut montrer que la convergence est encore vraie et que la normalité asymptotique est également vérifiée, avec la variance optimale, au sens où l'on atteint la covariance de l'algorithme statique. En pratique, cet algorithme est beaucoup moins sensible au choix des paramètres.
 L'algorithme de [82] a été introduit en 1952 pour estimer le maximum d'une fonction $f: x\mapsto \E[F(x,\xi)]$, connue à une perturbation près. Lorsque le gradient de $f$ n'est pas observable, cet algorithme permet d'approcher le maximum en utilisant une approximation du gradient de $f$ par des différences finies. Il est défini pour $n\geq 1$, par l'itération
L'algorithme de [82] a été introduit en 1952 pour estimer le maximum d'une fonction $f: x\mapsto \E[F(x,\xi)]$, connue à une perturbation près. Lorsque le gradient de $f$ n'est pas observable, cet algorithme permet d'approcher le maximum en utilisant une approximation du gradient de $f$ par des différences finies. Il est défini pour $n\geq 1$, par l'itération
 Il existe aussi des méthodes d'algorithmes stochastiques permettant de prendre en compte des espaces de contraintes. Parmi ces méthodes, l'algorithme de descente en miroir a l'avantage de ne pas nécessiter de recalculer à chaque itération une projection sur l'ensemble des contraintes.
Il existe aussi des méthodes d'algorithmes stochastiques permettant de prendre en compte des espaces de contraintes. Parmi ces méthodes, l'algorithme de descente en miroir a l'avantage de ne pas nécessiter de recalculer à chaque itération une projection sur l'ensemble des contraintes.
 A partir de la version déterministe de l'algorithme de descente en miroir introduite par [112], la version stochastique a été proposée par [114] et utilisée dans [145, 74] pour résoudre des problèmes d'optimisation convexe non-lisses et stochastiques. Récemment, de nouveaux algorithmes stochastiques d'approximation avec des propriétés de convergence fortes, basées sur la méthode Nesterov ont été proposées (voir par exemple [94, 113]). Tous ces algorithmes reposent sur l'existence d'un oracle stochastique, qui est un mécanisme pour générer des versions bruitées de la pente.
A partir de la version déterministe de l'algorithme de descente en miroir introduite par [112], la version stochastique a été proposée par [114] et utilisée dans [145, 74] pour résoudre des problèmes d'optimisation convexe non-lisses et stochastiques. Récemment, de nouveaux algorithmes stochastiques d'approximation avec des propriétés de convergence fortes, basées sur la méthode Nesterov ont été proposées (voir par exemple [94, 113]). Tous ces algorithmes reposent sur l'existence d'un oracle stochastique, qui est un mécanisme pour générer des versions bruitées de la pente.
 On munit $\Rset^d$ de la norme $L^1$ $\nrm{}$ et son espace dual $(\Rset^d)^*$ de la norme duale $\nrm{}_*$:
\[\nrm{x}=\sum_{i=1}^d \abs{x_i}, \quad \nrm{\xi}_*=\sup_{i=1, \ldots, d}\abs{\xi_i}.\]
Soit $C$ un sous-ensemble convexe compact de $\Rset^d$. L'algorithme stochastique de descente en miroir requiert l'utilisation d'une fonction auxiliaire qui est utilisé pour pousser la trajectoire dans l'ensemble de contraintes. A partir d'une fonction fortement convexe et différentiable notée $\delta$, on définit la fonction auxiliaire $V: \Rset^d \rightarrow \Rset$ par:
\[V(x)\egaldef \delta(x)-\delta(x_0)-\scal{\Delta\delta(x_0),x-x_0},\]
où $x_0$ est un point de $C$ et $\Delta$ désigne l'opérateur de gradient. Une fonction continue $\delta$ est dite fortement convexe de paramètre $\alpha$ si elle vérifie pour tout $\lambda \in [0,1]$:
\[\delta(\lambda x+(1-\lambda)y)\leq \lambda \delta(x)+(1-\lambda)\delta(y)-\frac{\alpha}{2}\lambda(1-\lambda)\nrm{x-y}^2.\]
Il est facile de voir que $V$ est fortement convexe. Soit $\beta>0$, on note $W_{\beta}$ la transformée de Fenchel-Legendre de $\beta V$:
\[W_{\beta}(\xi)=\sup_{x \in C}\left\{\scal{\xi,x}>-\beta V(x)\right\}.\]
L'algorithme de descente en miroir permet de trouver un extremum d'une fonction pour laquelle on n'a accès qu'à une version bruitée du gradient que l'on note $\psi$. Cet algorithme utilise deux suite positives $(\beta_n)$ et $(\gamma_n)$ et une suite d'observations vectorielles aléatoires $(\mathcal{Y}^n)$ de la façon suivante:
On munit $\Rset^d$ de la norme $L^1$ $\nrm{}$ et son espace dual $(\Rset^d)^*$ de la norme duale $\nrm{}_*$:
\[\nrm{x}=\sum_{i=1}^d \abs{x_i}, \quad \nrm{\xi}_*=\sup_{i=1, \ldots, d}\abs{\xi_i}.\]
Soit $C$ un sous-ensemble convexe compact de $\Rset^d$. L'algorithme stochastique de descente en miroir requiert l'utilisation d'une fonction auxiliaire qui est utilisé pour pousser la trajectoire dans l'ensemble de contraintes. A partir d'une fonction fortement convexe et différentiable notée $\delta$, on définit la fonction auxiliaire $V: \Rset^d \rightarrow \Rset$ par:
\[V(x)\egaldef \delta(x)-\delta(x_0)-\scal{\Delta\delta(x_0),x-x_0},\]
où $x_0$ est un point de $C$ et $\Delta$ désigne l'opérateur de gradient. Une fonction continue $\delta$ est dite fortement convexe de paramètre $\alpha$ si elle vérifie pour tout $\lambda \in [0,1]$:
\[\delta(\lambda x+(1-\lambda)y)\leq \lambda \delta(x)+(1-\lambda)\delta(y)-\frac{\alpha}{2}\lambda(1-\lambda)\nrm{x-y}^2.\]
Il est facile de voir que $V$ est fortement convexe. Soit $\beta>0$, on note $W_{\beta}$ la transformée de Fenchel-Legendre de $\beta V$:
\[W_{\beta}(\xi)=\sup_{x \in C}\left\{\scal{\xi,x}>-\beta V(x)\right\}.\]
L'algorithme de descente en miroir permet de trouver un extremum d'une fonction pour laquelle on n'a accès qu'à une version bruitée du gradient que l'on note $\psi$. Cet algorithme utilise deux suite positives $(\beta_n)$ et $(\gamma_n)$ et une suite d'observations vectorielles aléatoires $(\mathcal{Y}^n)$ de la façon suivante:
| Algorithme ${\bf 1}$ | |
| Initialisation : | $\displaystyle \left\{ \begin{array}{l} \xi_0=0\in (\Rset^d)^\star\\ \chi_0 \in C \end{array}\right. $ |
| Mise à jour : | pour $n = 1 , \ldots , N$ |
| $\displaystyle \left\{ \begin{array}{l} \xi_n = \xi_{n-1} -\gamma_n \Psi(\chi_{n-1} ,\mathcal{Y}^n)\\ \chi_n = \nabla W_{\beta_n}(\xi_n) \end{array} \right. $ | |
| Sortie : | $\displaystyle S_N = \frac{\sum_{n=1}^N \gamma_n \chi_{n-1}}{ \sum_{n=1}^N \gamma_n}$ |
 Ces techniques d'optimisation stochastique sont appliquées dans la suite du chapitre à plusieurs problèmes relatifs à l'estimation de médianes ainsi qu'à l'estimation d'une allocation optimale sous contrainte.
Ces techniques d'optimisation stochastique sont appliquées dans la suite du chapitre à plusieurs problèmes relatifs à l'estimation de médianes ainsi qu'à l'estimation d'une allocation optimale sous contrainte.
 Dans cette section, nous utilisons l'algorithme de Robbins-Monro pour l'estimation de médiane dans un espace de Hilbert ou pour la classification (non supervisée) à l'aide de $k$-médianes.
Dans cette section, nous utilisons l'algorithme de Robbins-Monro pour l'estimation de médiane dans un espace de Hilbert ou pour la classification (non supervisée) à l'aide de $k$-médianes.
 Pour une variable aléatoire réelle $Y$ à densité et de fonction de répartition strictement croissante, la médiane est définie comme étant l'unique valeur $m$ telle que
\[\E \left( \mbox{sign}(Y-m) \right) = 0 = \E\left( \frac{Y - m}{\abs{Y - m}}\right).\]
Il est ainsi naturel de définir la médiane comme étant
Pour une variable aléatoire réelle $Y$ à densité et de fonction de répartition strictement croissante, la médiane est définie comme étant l'unique valeur $m$ telle que
\[\E \left( \mbox{sign}(Y-m) \right) = 0 = \E\left( \frac{Y - m}{\abs{Y - m}}\right).\]
Il est ainsi naturel de définir la médiane comme étant
 Pour une généralisation dans un cadre multidimensionnel, étant donné que $\Rset^2$ n'a pas d'ordre naturel privilégié, la définition (3) suggère l'extension
Pour une généralisation dans un cadre multidimensionnel, étant donné que $\Rset^2$ n'a pas d'ordre naturel privilégié, la définition (3) suggère l'extension
 Des algorithmes itératifs d'estimation ont été proposés dans le cadre multivarié par [63] et [136], pour des variétés riemanniennes par [3], ainsi que par [60] pour des données fonctionnelles. Ce dernier algorithme nécessite d'inverser à chaque étape une matrice dont la dimension est égale à la dimension des données et nécessite donc d'importants efforts de calcul. L'algorithme proposé par [136] est beaucoup plus rapide et ne nécessite que $\mathcal{O}(nd)$ opérations à chaque itération, où $n$ est la taille de l'échantillon. Les propriétés de ces estimateurs figurent dans une étude détaillée récente de [110]. Ces procédures d'estimation ne sont pas adaptées lorsque les données arrivent séquentiellement, ils ont besoin de stocker toutes les données car la mise à jour nécessite toutes les observations antérieures.
Des algorithmes itératifs d'estimation ont été proposés dans le cadre multivarié par [63] et [136], pour des variétés riemanniennes par [3], ainsi que par [60] pour des données fonctionnelles. Ce dernier algorithme nécessite d'inverser à chaque étape une matrice dont la dimension est égale à la dimension des données et nécessite donc d'importants efforts de calcul. L'algorithme proposé par [136] est beaucoup plus rapide et ne nécessite que $\mathcal{O}(nd)$ opérations à chaque itération, où $n$ est la taille de l'échantillon. Les propriétés de ces estimateurs figurent dans une étude détaillée récente de [110]. Ces procédures d'estimation ne sont pas adaptées lorsque les données arrivent séquentiellement, ils ont besoin de stocker toutes les données car la mise à jour nécessite toutes les observations antérieures.
 La définition (4) est valable dans un espace vectoriel normé. Pour assurer l'unicité, la norme doit être strictement convexe (la boule unité doit l'être). Pour les espaces de Hilbert séparables et pour certains espaces de Banach comme $L^p$ pour $1<p<\infty$, [84] démontre que la médiane géométrique est unique dès que le support de la loi n'est pas contenu dans une droite.
La définition (4) est valable dans un espace vectoriel normé. Pour assurer l'unicité, la norme doit être strictement convexe (la boule unité doit l'être). Pour les espaces de Hilbert séparables et pour certains espaces de Banach comme $L^p$ pour $1<p<\infty$, [84] démontre que la médiane géométrique est unique dès que le support de la loi n'est pas contenu dans une droite.
 Dans les articles [25, 26, 20] nous considérons pour les applications l'espace de Hilbert séparable $H = L^2([0,T])$ de dimension infinie. On peut alors parler de «fonction médiane» d'une variable aléatoire à valeurs dans $H$. La médiane fonctionnelle a elle aussi de bonnes proriétés de robustesse. La détection automatique de courbes atypiques n'est pas facile en grande dimension. Estimer la médiane géométrique est par conséquent une alternative intéressante à la détection de courbes atypiques.
Dans les articles [25, 26, 20] nous considérons pour les applications l'espace de Hilbert séparable $H = L^2([0,T])$ de dimension infinie. On peut alors parler de «fonction médiane» d'une variable aléatoire à valeurs dans $H$. La médiane fonctionnelle a elle aussi de bonnes proriétés de robustesse. La détection automatique de courbes atypiques n'est pas facile en grande dimension. Estimer la médiane géométrique est par conséquent une alternative intéressante à la détection de courbes atypiques.
 On suppose que les hypothèses suivantes sont vérifiées.
On suppose que les hypothèses suivantes sont vérifiées.
- (A1) Le support de $Y$ n'est pas réduit à une droite.
- (A2) La loi de $Y$ est un mélange : $\mu_Y = \lambda\muDiff + (1-\lambda)\muDisc$, avec
- $\muDiff$ vérifie, $\forall x \in H, \muDiff( \{x\})=0$ et \[\alpha \mapsto \E \left( \| Y-\alpha \|^{-1} \right)\] est bornée uniformément sur les boules.
- $\muDisc$ est une mesure discrète qui ne charge pas la médiane $m$.
 La fonction à minimiser est $G: z\mapsto \E\left(\nrm{Y - z}\right)$.
La fonction à minimiser est $G: z\mapsto \E\left(\nrm{Y - z}\right)$.
| $ D_x G$ | $= -\E\left(\frac{Y - x}{\nrm{Y - x}}\right)$ |
| $ D^2_x G$ | $= \E\left(\frac{1}{\nrm{Y-x}}\left(\idt-\frac{( Y-x) \otimes (Y-x)}{\nrm{Y-x}^2}\right)\right),$ |
 On définit donc l'algorithme de Robbins-Monro d'estimation de la médiane de la façon suivante:
On définit donc l'algorithme de Robbins-Monro d'estimation de la médiane de la façon suivante:
 La moyennisation permet d'atteindre asymptotiquement au premier ordre la même variance que dans le cas de l'estimateur statique. De plus, l'algorithme de Robbins-Monro est vraiment très rapide. A titre indicatif, pour des simulations en dimension deux où $Y$ est un vecteur gaussien centré, en une seconde, on peut traiter des échantillons de taille :
La moyennisation permet d'atteindre asymptotiquement au premier ordre la même variance que dans le cas de l'estimateur statique. De plus, l'algorithme de Robbins-Monro est vraiment très rapide. A titre indicatif, pour des simulations en dimension deux où $Y$ est un vecteur gaussien centré, en une seconde, on peut traiter des échantillons de taille :
- $n=150$ avec l'algorithme de [136] (en R),
- $n=4500$ avec notre algorithme moyennisé (en R),
- $n=90\,000$ avec notre algorithme moyennisé (en C).
Quelques éléments de preuve: La preuve de la convergence est une application du théorème de Robbins Siegmund. Pour démontrer le théorème de la limite centrale, on utilise un premier résultat sur une majoration de la norme $L^2$ de l'erreur d'estimation. Ce premier résultat s'appuie sur une décomposition de l'algorithme sous la forme: \[Z_n-m=\beta_{n-1}(Z_1-m)+\beta_{n-1}M_n-\beta_{n-1}R_{n-1},\] où $\beta_n\egaldef (I_H-\gamma_{n}\Gamma_m)(I_H-\gamma_{n-1}\Gamma_m)\ldots (I_H-\gamma_{1}\Gamma_m)$, $M_n$ est la martingale définie par
 \[M_n\egaldef \sum_{k=1}^{n-1}\gamma_k \beta_k^{-1}\left(\Phi(Z_k)-\frac{Y_{k+1} - Z_k}{ \nrm{ Y_{k+1} - Z_k} }\right),\quad \Phi(x)\egaldef D_x G, \]
et le terme de reste $R_n$ est donné par
\[R_n\egaldef \sum_{k=1}^n \gamma_k \beta_k^{-1}\left(\Phi(Z_k)-\Gamma_m(Z_k-m)\right).\]
Avec une décomposition spectrale, on contrôle le terme déterministe $\beta_{n-1}$. On utilise ensuite la structure de martingale pour contrôler la vitesse de convergence de la martingale et on montre avec la décomposition spectrale que le terme de reste est bien un reste.
\[M_n\egaldef \sum_{k=1}^{n-1}\gamma_k \beta_k^{-1}\left(\Phi(Z_k)-\frac{Y_{k+1} - Z_k}{ \nrm{ Y_{k+1} - Z_k} }\right),\quad \Phi(x)\egaldef D_x G, \]
et le terme de reste $R_n$ est donné par
\[R_n\egaldef \sum_{k=1}^n \gamma_k \beta_k^{-1}\left(\Phi(Z_k)-\Gamma_m(Z_k-m)\right).\]
Avec une décomposition spectrale, on contrôle le terme déterministe $\beta_{n-1}$. On utilise ensuite la structure de martingale pour contrôler la vitesse de convergence de la martingale et on montre avec la décomposition spectrale que le terme de reste est bien un reste.
 Pour prouver le théorème de la limite centrale à partir de la majoration de la vitesse on utilise une autre décomposition de l'algorithme moyennisé:
\[n\Gamma_m\left(\overline{Z}_n-m\right)=\sum_{k=1}^n\frac{1}{\gamma_k}(Z_k-Z_{k+1})-\sum_{k=1}^n\left(\Phi(Z_k)-\Gamma_m(Z_k-m)\right)+\widetilde{M}_{n+1},\]
avec la martingale
\[\widetilde{M}_{n+1}\egaldef \sum_{k=1}^n\left(\Phi(Z_k)-\frac{Y_{k+1} - Z_k}{ \nrm{ Y_{k+1} - Z_k} }\right).\]
On montre dans un premier temps que le théorème de la limite centrale pour les martingales à valeurs dans un espace de Hilbert s'applique pour notre martingale, puis que les autres termes sont négligeables grâce à la majoration obtenue avec la première décomposition.
Pour prouver le théorème de la limite centrale à partir de la majoration de la vitesse on utilise une autre décomposition de l'algorithme moyennisé:
\[n\Gamma_m\left(\overline{Z}_n-m\right)=\sum_{k=1}^n\frac{1}{\gamma_k}(Z_k-Z_{k+1})-\sum_{k=1}^n\left(\Phi(Z_k)-\Gamma_m(Z_k-m)\right)+\widetilde{M}_{n+1},\]
avec la martingale
\[\widetilde{M}_{n+1}\egaldef \sum_{k=1}^n\left(\Phi(Z_k)-\frac{Y_{k+1} - Z_k}{ \nrm{ Y_{k+1} - Z_k} }\right).\]
On montre dans un premier temps que le théorème de la limite centrale pour les martingales à valeurs dans un espace de Hilbert s'applique pour notre martingale, puis que les autres termes sont négligeables grâce à la majoration obtenue avec la première décomposition.
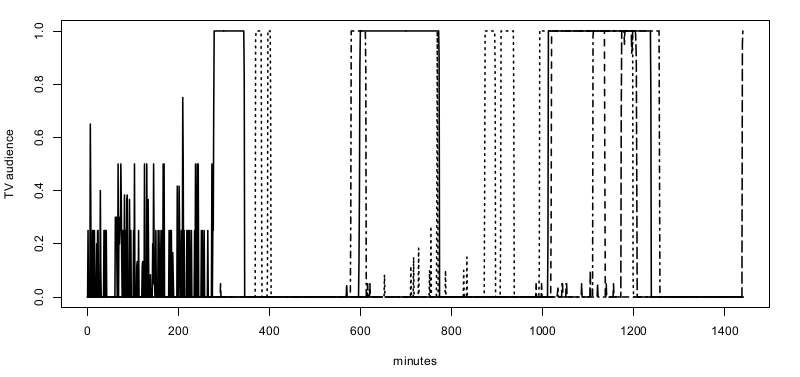
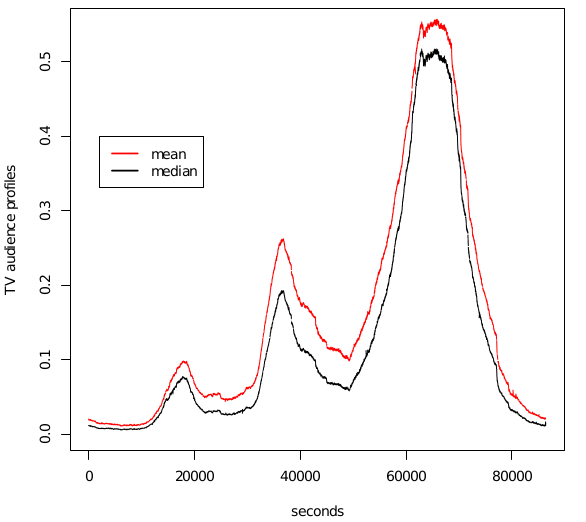
 La société Médiamétrie nous a fourni leurs données sur les audiences télévisuelles pour la journée du 6 septembre 2010. Après avoir supprimé de l'échantillon les données des individus n'ayant pas allumé leur poste ce jour là, le jeu de données contient $n=5423$ courbes d'audience. Pour chaque courbe, nous avons un vecteur $Y_i \in \{0,1\}^{86400}$ où $86400$ est le nombre de secondes dans une journée. Chaque seconde $Y_i$ vaut $1$ à la seconde $s$ si l'individu $i$ regarde la télévision à cet instant et $0$ sinon. La Figure 3 représente un exemple de profil d'audience sur une journée.
La société Médiamétrie nous a fourni leurs données sur les audiences télévisuelles pour la journée du 6 septembre 2010. Après avoir supprimé de l'échantillon les données des individus n'ayant pas allumé leur poste ce jour là, le jeu de données contient $n=5423$ courbes d'audience. Pour chaque courbe, nous avons un vecteur $Y_i \in \{0,1\}^{86400}$ où $86400$ est le nombre de secondes dans une journée. Chaque seconde $Y_i$ vaut $1$ à la seconde $s$ si l'individu $i$ regarde la télévision à cet instant et $0$ sinon. La Figure 3 représente un exemple de profil d'audience sur une journée.
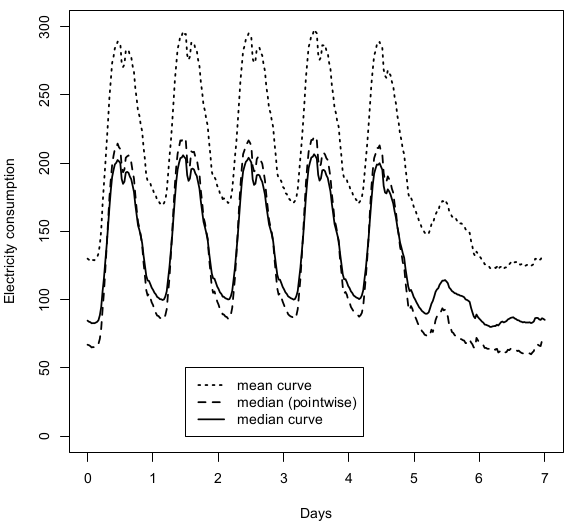
 Dans [39], nous analysons un échantillon de plus de $18902$ courbes de consommation d'électricité mesurées chaque demi-heure sur une période d'une semaine. On représente sur la Figure 5 la courbe moyenne de consommation ainsi que la courbe médiane. La différence marquée entre les deux courbes est dûe à la présence d'une petite fraction de clients possédant une très grande consommation électrique.
Dans [39], nous analysons un échantillon de plus de $18902$ courbes de consommation d'électricité mesurées chaque demi-heure sur une période d'une semaine. On représente sur la Figure 5 la courbe moyenne de consommation ainsi que la courbe médiane. La différence marquée entre les deux courbes est dûe à la présence d'une petite fraction de clients possédant une très grande consommation électrique.
 On souhaite maintenant prendre en compte des variables corrélées avec la variable étudiée. L'estimation de la façon dont la forme de la courbe peut dépendre de variables réelles ou fonctionnelles donne lieu à une vaste littérature. Le principal inconvénient de tous ces estimateurs est qu'ils dépendent tous, explicitement ou non, d'une méthode basée sur les moindres carrés et sont donc sensibles aux valeurs atypiques aberrantes.
On souhaite maintenant prendre en compte des variables corrélées avec la variable étudiée. L'estimation de la façon dont la forme de la courbe peut dépendre de variables réelles ou fonctionnelles donne lieu à une vaste littérature. Le principal inconvénient de tous ces estimateurs est qu'ils dépendent tous, explicitement ou non, d'une méthode basée sur les moindres carrés et sont donc sensibles aux valeurs atypiques aberrantes.
 Soit $(Y,X)$ une paire de variables aléatoires à valeurs dans $H\times \Rset$. On suppose que $X$ est une variable continue. On veut estimer la médiane géométrique de $Y$ conditionnellement à $X=x$, c'est-à-dire la valeur $m(x)$ définie par
\[m(x)=\argmin_{\alpha \in H} \E[\nrm{Y-\alpha} - \nrm{Y} | X=x].\]
De même que dans le cas non conditionné, il y a existence et unicité de $m(x)$ dès que le support de $Y$ sachant $X=x$ n'est pas contenu dans une droite.
Soit $(Y,X)$ une paire de variables aléatoires à valeurs dans $H\times \Rset$. On suppose que $X$ est une variable continue. On veut estimer la médiane géométrique de $Y$ conditionnellement à $X=x$, c'est-à-dire la valeur $m(x)$ définie par
\[m(x)=\argmin_{\alpha \in H} \E[\nrm{Y-\alpha} - \nrm{Y} | X=x].\]
De même que dans le cas non conditionné, il y a existence et unicité de $m(x)$ dès que le support de $Y$ sachant $X=x$ n'est pas contenu dans une droite.
 On introduit un algorithme pondéré par un noyau pour prendre en compte les covariables. L'algorithme de la médiane géométrique (5) devient pour la médiane géométrique conditionnelle:
\[
Z_{n+1}(x) = Z_{n}(x) + \gamma_n \frac{Y_{n+1} - Z_{n}(x)}{\nrm{Y_{n+1} - Z_{n}(x)}} \frac{1}{h_n} K \left( \frac{X_{n+1}-x}{h_n}\right)
\]
avec les deux suites déterministes $(h_n)$ et $(\gamma_n)$ et le noyau $K$ en paramètres.
On introduit un algorithme pondéré par un noyau pour prendre en compte les covariables. L'algorithme de la médiane géométrique (5) devient pour la médiane géométrique conditionnelle:
\[
Z_{n+1}(x) = Z_{n}(x) + \gamma_n \frac{Y_{n+1} - Z_{n}(x)}{\nrm{Y_{n+1} - Z_{n}(x)}} \frac{1}{h_n} K \left( \frac{X_{n+1}-x}{h_n}\right)
\]
avec les deux suites déterministes $(h_n)$ et $(\gamma_n)$ et le noyau $K$ en paramètres.
On suppose que les hypothèses suivantes sont satisfaites.
- Le noyau $K$ est symétrique autour de $0$, positif, à support compact,
$ \int_\Rset K(u) du$ $= 1$ $ \int_\Rset K(u)^2 du = \nu^2.$ - Pour tout $x$ dans le support de la densité de $X$, la variable $Y$ sachant $X=x$ n'est pas concentrée sur une droite.
- La densité $p(x)$ de la loi de $X$ est à support borné, continue, deux fois différentiable avec les dérivées bornées.
- Les lois conditionnelles $\mu_x = \law(Y|X = x)$ varient régulièrement en fonction de $x$: il existe deux constantes $c$ et $\beta$ telles que \[ \wass{\mu_x, \mu_{x'}} \leq c\abs{x-x'}^\beta,\] où $\wass{\mu_x, \mu_{x'}}$ désigne la distance de Wasserstein entre $\mu_x$ et $\mu_{x'}$.
- Il existe une constante $C$ telle que \[ \forall \alpha \in H, \forall x\in \Rset, \E[\nrm{Y-\alpha}^{-2} | X=x] \leq C. \]
 On définit l'algorithme moyennisé $\overline{Z}_{n+1}(x) = \frac{1}{n} \sum_{k=1}^n Z_k(x)$ et on choisit des suites de pas sous la forme
On définit l'algorithme moyennisé $\overline{Z}_{n+1}(x) = \frac{1}{n} \sum_{k=1}^n Z_k(x)$ et on choisit des suites de pas sous la forme
| $\gamma_n$ | $= \frac{c_\gamma}{n^\gamma},$ | $h_n$ | $= \frac{c_h}{n^h}.$(7) |
 Comme pour la médiane, la preuve consiste en une décomposition spectrale minutieuse ainsi qu'une application du théorème de Robbins-Siegmund. On utilise de nouveau une approche de type forward permettant de dégager une martingale et d'utiliser le TLC pour martingales hilbertiennes. Enfin, ce théorème est une nouvelle fois une conséquence du théorème de Thalès.
Comme pour la médiane, la preuve consiste en une décomposition spectrale minutieuse ainsi qu'une application du théorème de Robbins-Siegmund. On utilise de nouveau une approche de type forward permettant de dégager une martingale et d'utiliser le TLC pour martingales hilbertiennes. Enfin, ce théorème est une nouvelle fois une conséquence du théorème de Thalès.
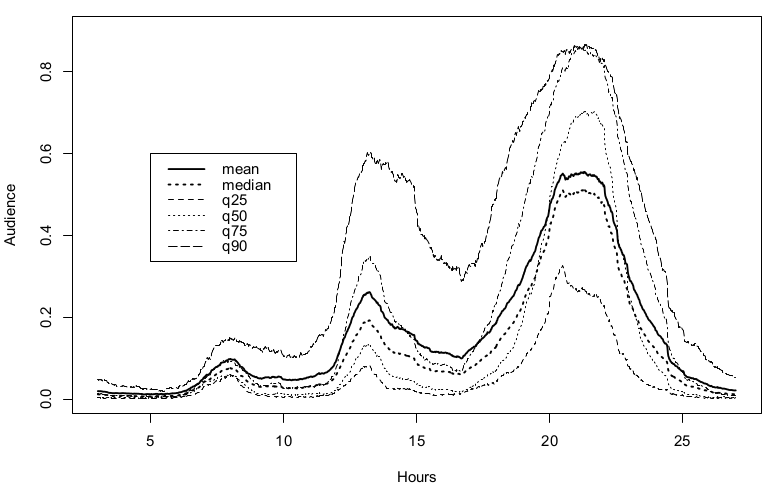
 On utilise cet algorithme sur les mêmes données de Médiamétrie pour estimer un profil d'audience télévisuel médian, conditionné par le temps total passé à regarder la télévision. On cherche à estimer les comportements de consommation de télévision, sur une période de $24$ heures. La covariable $X$ représente ici la proportion du temps passé devant la télévision la journée du 6 Septembre 2010. On considère les valeurs quantiles de la covariable $X$ qui sont, pour notre échantillon, $q_{25}=0,0599$, $q_{50}=0,128$, $q_{75}= 0,225$ et $q_{90}=0,348$. Cela signifie par exemple que les dix pour cent des individus avec les niveaux d'audience les plus élevés passent plus de $34,8\%$ de leur temps à regarder la télévision alors que $25\%$ des individus passent moins de $6\%$ de leur temps à regarder la télévision.
On utilise cet algorithme sur les mêmes données de Médiamétrie pour estimer un profil d'audience télévisuel médian, conditionné par le temps total passé à regarder la télévision. On cherche à estimer les comportements de consommation de télévision, sur une période de $24$ heures. La covariable $X$ représente ici la proportion du temps passé devant la télévision la journée du 6 Septembre 2010. On considère les valeurs quantiles de la covariable $X$ qui sont, pour notre échantillon, $q_{25}=0,0599$, $q_{50}=0,128$, $q_{75}= 0,225$ et $q_{90}=0,348$. Cela signifie par exemple que les dix pour cent des individus avec les niveaux d'audience les plus élevés passent plus de $34,8\%$ de leur temps à regarder la télévision alors que $25\%$ des individus passent moins de $6\%$ de leur temps à regarder la télévision.
 Sur la Figure 6, on représente les estimations des médianes conditionnelles avec une bande passante réglée sur $h_n=0,05$ et un paramètre de descente $c_{\gamma}=0,5$, pour $x\in\{q_{25}, q_{50}, q_{75}, q_{90}\}$. On peut noter que la forme des profils conditionnés dépend fortement de la valeur de la covariable: par exemple, les courbes médianes conditionnées à $x=q_{75}$ et $x=q_{90}$ sont vraiment distinctes en particulier aux instants $15$ et $21$. D'un point de vue rapidité de calcul, pour un point de départ donné, notre algorithme, qui prend moins de deux secondes, est environ $70$ fois plus rapide que l'estimateur statique qui exige $140$ secondes pour converger.
Sur la Figure 6, on représente les estimations des médianes conditionnelles avec une bande passante réglée sur $h_n=0,05$ et un paramètre de descente $c_{\gamma}=0,5$, pour $x\in\{q_{25}, q_{50}, q_{75}, q_{90}\}$. On peut noter que la forme des profils conditionnés dépend fortement de la valeur de la covariable: par exemple, les courbes médianes conditionnées à $x=q_{75}$ et $x=q_{90}$ sont vraiment distinctes en particulier aux instants $15$ et $21$. D'un point de vue rapidité de calcul, pour un point de départ donné, notre algorithme, qui prend moins de deux secondes, est environ $70$ fois plus rapide que l'estimateur statique qui exige $140$ secondes pour converger.
 Pour résumer cette première partie, l'algorithme de gradient stochastique permettant d'estimer la médiane d'une distribution à valeurs dans un espace de Hilbert est un algorithme très simple à mettre en place, peu sensible au choix des paramètres lorsque l'on utilise la version moyennisée, très rapide en temps d'exécution pour une vitesse de convergence optimale, au sens où l'on atteint la covariance de l’algorithme statique.
Pour résumer cette première partie, l'algorithme de gradient stochastique permettant d'estimer la médiane d'une distribution à valeurs dans un espace de Hilbert est un algorithme très simple à mettre en place, peu sensible au choix des paramètres lorsque l'on utilise la version moyennisée, très rapide en temps d'exécution pour une vitesse de convergence optimale, au sens où l'on atteint la covariance de l’algorithme statique.
 Classifier rapidement de gros échantillons en grande dimension est un enjeu important en statistique computationnelle et en apprentissage, avec des domaines d'applications variés. La littérature sur les techniques de classification est riche comme en attestent les études référencées sur le sujet de [73] et [59]. De plus, comme il est souligné dans [16], le développement d'algorithmes rapides est d'autant plus important que le temps de calcul est limité et l'échantillon important, étant donné que des procédures rapides seront en mesure de traiter un plus grand nombre d'observations et finiront par fournir de meilleures estimations que les plus lentes.
Classifier rapidement de gros échantillons en grande dimension est un enjeu important en statistique computationnelle et en apprentissage, avec des domaines d'applications variés. La littérature sur les techniques de classification est riche comme en attestent les études référencées sur le sujet de [73] et [59]. De plus, comme il est souligné dans [16], le développement d'algorithmes rapides est d'autant plus important que le temps de calcul est limité et l'échantillon important, étant donné que des procédures rapides seront en mesure de traiter un plus grand nombre d'observations et finiront par fournir de meilleures estimations que les plus lentes.
 On souhaite trouver une partition de $\Rset^d$ en $k$ ensembles (classes) homogènes. Le nombre de classes est fixé à l'avance. Chaque classe est caractérisée par son centre $\boldsymbol{\theta}^\ell \in \Rset^d,$ $\ell=1, \ldots, k,$ en minimisant la fonction $g : \Rset^{dk} \mapsto \Rset$ définie par
On souhaite trouver une partition de $\Rset^d$ en $k$ ensembles (classes) homogènes. Le nombre de classes est fixé à l'avance. Chaque classe est caractérisée par son centre $\boldsymbol{\theta}^\ell \in \Rset^d,$ $\ell=1, \ldots, k,$ en minimisant la fonction $g : \Rset^{dk} \mapsto \Rset$ définie par
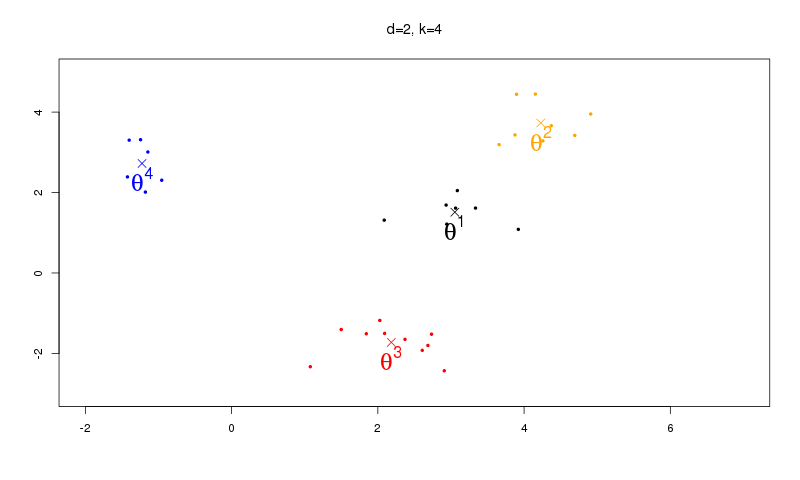
 Nous nous intéressons dans cette section au cas où l'on cherche à minimiser la norme $L^1$, c'est-à-dire $\varphi(u) = |u|,$ dans (9). Nous effectuons un algorithme de type $k$-médianes; les centres des classes sont les points médians de la classe. Cette approche est une première tentative pour obtenir des algorithmes de classification plus robustes, suggérée par [99] et développée par [81]. Il a été prouvé dans [91] que, sous des hypothèses générales, le minimum de la fonction objectif est unique. De nombreux algorithmes ont été proposés dans la littérature pour trouver ce minimum.
Nous nous intéressons dans cette section au cas où l'on cherche à minimiser la norme $L^1$, c'est-à-dire $\varphi(u) = |u|,$ dans (9). Nous effectuons un algorithme de type $k$-médianes; les centres des classes sont les points médians de la classe. Cette approche est une première tentative pour obtenir des algorithmes de classification plus robustes, suggérée par [99] et développée par [81]. Il a été prouvé dans [91] que, sous des hypothèses générales, le minimum de la fonction objectif est unique. De nombreux algorithmes ont été proposés dans la littérature pour trouver ce minimum.
 Dans [20] nous proposons une stratégie récursive de type $k$-médianes pour estimer les centres des classes. L'un des principaux avantages de notre estimateur est qu'il peut être calculé en seulement $\mathcal{O}(kn)$ opérations et permet donc de traiter de grandes bases de données. Par sa nature récursive, il permet une mise à jour automatique et n'a pas besoin de stocker toutes les données. Enfin, il est plus robuste que l'estimateur des k-means.
Dans [20] nous proposons une stratégie récursive de type $k$-médianes pour estimer les centres des classes. L'un des principaux avantages de notre estimateur est qu'il peut être calculé en seulement $\mathcal{O}(kn)$ opérations et permet donc de traiter de grandes bases de données. Par sa nature récursive, il permet une mise à jour automatique et n'a pas besoin de stocker toutes les données. Enfin, il est plus robuste que l'estimateur des k-means.
 On dispose d'un échantillon $X_1, \ldots, X_N$ de vecteurs aléatoires indépendants et identiquement distribués de $\Rset^d$.
On dispose d'un échantillon $X_1, \ldots, X_N$ de vecteurs aléatoires indépendants et identiquement distribués de $\Rset^d$.
 On note $I_\ell$ l'indicatrice d'appartenance d'un point $\mathbf{x} \in \Rset^d$ à la classe $\ell,$
\[I_\ell(\mathbf{x}, \boldsymbol{\theta})=\prod_{j=1}^{k}\ind{\|\mathbf{x}-\boldsymbol{\theta}^\ell \| \leq \| \mathbf{x}-\boldsymbol{\theta}^j \|}.\]
L'algorithme des $k$-means est défini de la façon suivante. Pour la phase d'initialisation, on choisit arbitrairement $k$ points initiaux de $\Rset^d$ notés $\boldsymbol{\theta}^\ell_1$. On effectue ensuite la phase d'itération de type algorithme de gradient stochastique
\[\btheta_{n+1}^\ell=\btheta_n^\ell -a_n^\ell I_\ell(\mathbf{X}_n, \btheta_n) \left(\btheta_n^\ell -\mathbf{X}_n \right),\]
où pour $n\geq 1$,
\[a_n^\ell\egaldef (1+n_{\ell})^{-1}\quad \mbox{et}\quad n_{\ell}\egaldef 1+\sum_{r=1}^{n-1}I_\ell(\mathbf{X}_r, \btheta_r).\]
Avec cet algorithme, les centres de classes à la $n$-ième itération sont tout simplement la moyenne des points attribués à cette classe:
\[
\btheta_{n+1}^\ell = \frac{1}{1 + n_\ell} \left( \btheta_1^\ell+ \sum_{i=1}^n I_\ell(\mathbf{X}_i;\btheta_i) \mathbf{X}_i \right).
\]
On note $I_\ell$ l'indicatrice d'appartenance d'un point $\mathbf{x} \in \Rset^d$ à la classe $\ell,$
\[I_\ell(\mathbf{x}, \boldsymbol{\theta})=\prod_{j=1}^{k}\ind{\|\mathbf{x}-\boldsymbol{\theta}^\ell \| \leq \| \mathbf{x}-\boldsymbol{\theta}^j \|}.\]
L'algorithme des $k$-means est défini de la façon suivante. Pour la phase d'initialisation, on choisit arbitrairement $k$ points initiaux de $\Rset^d$ notés $\boldsymbol{\theta}^\ell_1$. On effectue ensuite la phase d'itération de type algorithme de gradient stochastique
\[\btheta_{n+1}^\ell=\btheta_n^\ell -a_n^\ell I_\ell(\mathbf{X}_n, \btheta_n) \left(\btheta_n^\ell -\mathbf{X}_n \right),\]
où pour $n\geq 1$,
\[a_n^\ell\egaldef (1+n_{\ell})^{-1}\quad \mbox{et}\quad n_{\ell}\egaldef 1+\sum_{r=1}^{n-1}I_\ell(\mathbf{X}_r, \btheta_r).\]
Avec cet algorithme, les centres de classes à la $n$-ième itération sont tout simplement la moyenne des points attribués à cette classe:
\[
\btheta_{n+1}^\ell = \frac{1}{1 + n_\ell} \left( \btheta_1^\ell+ \sum_{i=1}^n I_\ell(\mathbf{X}_i;\btheta_i) \mathbf{X}_i \right).
\]
 Pour notre algorithme des $k$-médianes, les centres de classes sont les points médians (au sens de la médiane géométrique) de leur classe. On modifie donc l'algorithme précédent dans sa phase d'itération pour $n \geq 1,$ et $\ell=1, \ldots, k,$ pour construire l'algorithme de $k$-médianes:
Pour notre algorithme des $k$-médianes, les centres de classes sont les points médians (au sens de la médiane géométrique) de leur classe. On modifie donc l'algorithme précédent dans sa phase d'itération pour $n \geq 1,$ et $\ell=1, \ldots, k,$ pour construire l'algorithme de $k$-médianes:
- (H1)
- Le vecteur aléatoire $X$ a une densité absolument continue.
- $X$ est borné : $\exists K>0$: $\nrm{X}\leq K$ p.s. g
- $\exists C$ tel que: $\forall x \in \Rset^{d}$ satisfaisant $\nrm{x}\leq K+1$, $\E\left[\frac{1}{\nrm{X-x}}\right]<C$.
- (H2)
- $\forall n \geq 1$, $\displaystyle\min_\ell a_n^\ell>0$.
- $\displaystyle\max_\ell \sup_n a_n^\ell < \min(\frac12, \frac{1}{8C})$ p.s.
- $\displaystyle\sum_{n=1}^{\infty}\max_\ell a_n^\ell=\infty$ p.s.
- $ \displaystyle\sup_{n}\frac{\max_\ell a_n^\ell}{\min_\ell a_n^\ell}<\infty \quad \mbox{p.s.}$
- (H3) $\displaystyle\sum_{\ell=1}^k\sum_{n=1}^{\infty}\left(a_n^\ell\right)^2<\infty \quad \mbox{p.s.}$
- (H3') $\displaystyle\sum_{\ell=1}^k\sum_{n=1}^{\infty}\E\left[\left(a_n^\ell \right)^2I_\ell (X_n,\btheta_n)\right]<\infty .$
 Nous avons établi des profils d'audience du $6$ Septembre $2010$, à partir d'un échantillon de $n= 5422$ audiences individuelles, regroupées pour toutes les chaînes de télévision et mesurée toutes les minutes sur une période de 24 heures. Un échantillon de $5$ profils temporels différents est représenté sur la Figure 8.
Nous avons établi des profils d'audience du $6$ Septembre $2010$, à partir d'un échantillon de $n= 5422$ audiences individuelles, regroupées pour toutes les chaînes de télévision et mesurée toutes les minutes sur une période de 24 heures. Un échantillon de $5$ profils temporels différents est représenté sur la Figure 8.
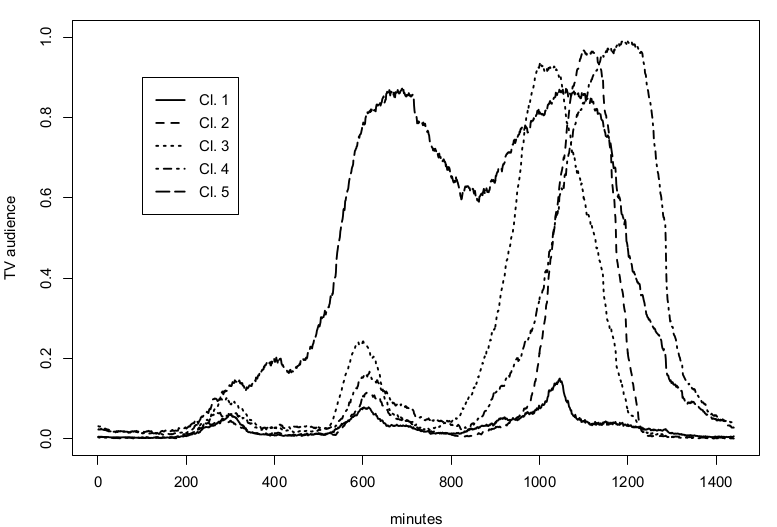
Dans la dernière partie de ce chapitre, on utilise un autre algorithme de gradient stochastique, l'algorithme de descente en miroir, appliqué à un problème d'allocation optimale.
 Les nouvelles règles de régulation du secteur de l'assurance, appelées en Europe « Solvency 2 », conduisent les entreprises à ajuster leurs marges de solvabilité aux risques sous-jacents. Le capital global $u$ doit être réparti pour chaque secteur d'activité: $u_k$ est le capital initial de la ligne $k$ de l'entreprise et $u_1+\ldots+u_d=u$, où $d$ est le nombre de lignes de l'entreprise. Il s'agit donc de trouver, à partir d'un capital $u$ fixé, l'allocation optimale minimisant certains indicateurs de risque.
Les nouvelles règles de régulation du secteur de l'assurance, appelées en Europe « Solvency 2 », conduisent les entreprises à ajuster leurs marges de solvabilité aux risques sous-jacents. Le capital global $u$ doit être réparti pour chaque secteur d'activité: $u_k$ est le capital initial de la ligne $k$ de l'entreprise et $u_1+\ldots+u_d=u$, où $d$ est le nombre de lignes de l'entreprise. Il s'agit donc de trouver, à partir d'un capital $u$ fixé, l'allocation optimale minimisant certains indicateurs de risque.
 On considère un processus vectoriel de risque $X_n=(X_n^1, \ldots, X_n^d)^{t}$, où $X_n^k$ désigne les gains (c'est-à-dire les revenus auxquels on soustrait les pertes) de la ligne $k$ pendant la période $n$. On note les gains cumulés
\[Y_n^k=\sum_{p=1}^nX_p^k.\]
On dit que la $k$ème ligne de l'entreprise fait défaut avant l'instant $n$ s'il existe $i\in \{1,\ldots, n\}$ tel que $Y_i^k + u_k<0$. On note $R_n^k=u_k+Y_n^k$ le capital de la ligne $k$ de l'entreprise à l'instant $n$.
On considère un processus vectoriel de risque $X_n=(X_n^1, \ldots, X_n^d)^{t}$, où $X_n^k$ désigne les gains (c'est-à-dire les revenus auxquels on soustrait les pertes) de la ligne $k$ pendant la période $n$. On note les gains cumulés
\[Y_n^k=\sum_{p=1}^nX_p^k.\]
On dit que la $k$ème ligne de l'entreprise fait défaut avant l'instant $n$ s'il existe $i\in \{1,\ldots, n\}$ tel que $Y_i^k + u_k<0$. On note $R_n^k=u_k+Y_n^k$ le capital de la ligne $k$ de l'entreprise à l'instant $n$.
 On considère un indicateur de risque permettant de tenir compte à la fois de la structure de dépendance entre les secteurs d'activité et de la gravité (ou du coût) de l'insolvabilité. A partir des fonctions de coût, convexes, $g_k: \Rset\rightarrow \Rset$, $k=1, \ldots, d$ satisfaisant $g_k(x)\geq 0$ pour $x\leq 0$, et $\E(|g_k(R_p^k)|)<\infty$, on considère l'indicateur de risque
\[I(u_1 ,\ldots , u_d) = \sum_{k=1}^d \E\left(\sum_{p=1}^n g_k(R_p^k) \ind{R_p^k<0} \ind{\sum_{j=1}^d R_p^j>0}\right) .\]
La fonction $g_k$ représente le coût que la branche d'activité $k$ doit payer quand elle devient insolvable. Minimiser $I$ permet de contrôler l'insolvabilité partielle, c'est-à-dire l'insolvabilité mesurée pour certaines branches alors que l'ensemble de l'entreprise est solvable. Un choix naturel pour le coût pourrait être $g_k(x)=-x$. Le graphique ci-après représente l'indicateur de risque $I$ (zone claire) pour $g_k(x)=-x$ et $d = 2$.
On considère un indicateur de risque permettant de tenir compte à la fois de la structure de dépendance entre les secteurs d'activité et de la gravité (ou du coût) de l'insolvabilité. A partir des fonctions de coût, convexes, $g_k: \Rset\rightarrow \Rset$, $k=1, \ldots, d$ satisfaisant $g_k(x)\geq 0$ pour $x\leq 0$, et $\E(|g_k(R_p^k)|)<\infty$, on considère l'indicateur de risque
\[I(u_1 ,\ldots , u_d) = \sum_{k=1}^d \E\left(\sum_{p=1}^n g_k(R_p^k) \ind{R_p^k<0} \ind{\sum_{j=1}^d R_p^j>0}\right) .\]
La fonction $g_k$ représente le coût que la branche d'activité $k$ doit payer quand elle devient insolvable. Minimiser $I$ permet de contrôler l'insolvabilité partielle, c'est-à-dire l'insolvabilité mesurée pour certaines branches alors que l'ensemble de l'entreprise est solvable. Un choix naturel pour le coût pourrait être $g_k(x)=-x$. Le graphique ci-après représente l'indicateur de risque $I$ (zone claire) pour $g_k(x)=-x$ et $d = 2$.
 Il s'agit donc de déterminer un minimum sous contraintes: trouver $u^\star \in (\Rset_+)^d$ tel que
Il s'agit donc de déterminer un minimum sous contraintes: trouver $u^\star \in (\Rset_+)^d$ tel que
 Alors que les algorithmes de Robbins-Monro et Kiefer-Wolfowitz sont très sensibles au choix du pas, il est remarquable que notre version de descente en miroir d'un algorithme de type Kiefer-Wolfowitz soit très stable et permette des simulations en grande dimension. Enfin, notre algorithme permet de prendre en compte une dépendance temporelle sur une période de longueur $p$. Néanmoins, pour faire tourner l'algorithme, il faut posséder $N$ copies indépendantes de la distribution des gains sur une période de longueur $p$.
Alors que les algorithmes de Robbins-Monro et Kiefer-Wolfowitz sont très sensibles au choix du pas, il est remarquable que notre version de descente en miroir d'un algorithme de type Kiefer-Wolfowitz soit très stable et permette des simulations en grande dimension. Enfin, notre algorithme permet de prendre en compte une dépendance temporelle sur une période de longueur $p$. Néanmoins, pour faire tourner l'algorithme, il faut posséder $N$ copies indépendantes de la distribution des gains sur une période de longueur $p$.
 Pour une réalisation $y$ de la matrice aléatoire
\[\mathcal{Y}= \begin{pmatrix}
Y_1^1 & \cdots & Y_p^1 \\
\cdots & \cdots & \cdots \\
Y_1^d & \cdots & Y_p^d
\end{pmatrix}\]
on pose
\[\mathcal{I}(u_1 , \ldots , u_d , y) = \sum_{k=1}^d\sum_{n=1}^p g_k(y_n^k+u_k )\ind{y_n^k+u_k<0}\ind{\sum_{k=1}^d y_n^k +u_k >0} ,\]
de sorte que
\[I(u_1, \ldots , u_d)=\sum_{k=1}^d\E\left(\sum_{n=1}^p g_k(R_n^k) \ind{R_n^k<0}\ind{\sum_{k=1}^d R_n^k>0}\right).\]
On note également, pour une suite $(c_n)$ convenablement choisie:
Pour une réalisation $y$ de la matrice aléatoire
\[\mathcal{Y}= \begin{pmatrix}
Y_1^1 & \cdots & Y_p^1 \\
\cdots & \cdots & \cdots \\
Y_1^d & \cdots & Y_p^d
\end{pmatrix}\]
on pose
\[\mathcal{I}(u_1 , \ldots , u_d , y) = \sum_{k=1}^d\sum_{n=1}^p g_k(y_n^k+u_k )\ind{y_n^k+u_k<0}\ind{\sum_{k=1}^d y_n^k +u_k >0} ,\]
de sorte que
\[I(u_1, \ldots , u_d)=\sum_{k=1}^d\E\left(\sum_{n=1}^p g_k(R_n^k) \ind{R_n^k<0}\ind{\sum_{k=1}^d R_n^k>0}\right).\]
On note également, pour une suite $(c_n)$ convenablement choisie:
| $ \mathcal{I}^k\left(c_n^+,\mathcal{Y}\right)$ | $=$ | $\mathcal{I}(\chi^{1}_{n-1}, \ldots, \chi^{k-1}_{n-1},\chi^{k}_{n-1} +c_n,\chi^{k+1}_{n-1}, \ldots, \chi^{d}_{n-1}, \mathcal{Y}),$ |
| $ \mathcal{I}^k\left(c_n^-,\mathcal{Y}\right)$ | $=$ | $\mathcal{I}(\chi^{1}_{n-1}, \ldots, \chi^{k-1}_{n-1},\chi^{k}_{n-1} -c_n,\chi^{k+1}_{n-1}, \ldots, \chi^{d}_{n-1}, \mathcal{Y}).$ |
| Algorithme ${\bf 2}$ | |
| Initialisation : | $\displaystyle \left\{ \begin{array}{l} \xi_0=0\in (\Rset^m)^\star\\ \chi_0 \in C \end{array}\right. $ |
| Mise à jour : | pour $n = 1 , \ldots , N$ |
| $\displaystyle \left\{ \begin{array}{l} \xi_n = \xi_{n-1} -\gamma_n \Psi_{c_n}(\chi_{n-1} ,\mathcal{Y}_n)\\ \chi_n = \nabla W_{\beta_n}(\xi_n) \end{array} \right. $ | |
| Sortie : | $\displaystyle S_N = \frac{\sum_{n=1}^N \gamma_n \chi_{n-1}}{ \sum_{n=1}^N \gamma_n}$ |
- (1) $I$ est une fonction convexe de $\Rset^d$ dans $\Rset$.
- (2) $I$ est de classe $C^2$.
- (3) $I$ admet un unique minimum $x^*$ sur $C$.
- (4) Il existe un réel positif $\sigma$ tel que pour tout vecteur $(v_1,\ldots, v_d)\in \Rset^d$, \[\var{\left(\mathcal{I}(v_1,\ldots, v_d,\mathcal{Y}_n)|\mathcal{F}_{n-1}\right)}\leq \sigma^2,\] où $\mathcal{F}_n$ désigne la tribu engendrée par $\left(\chi_0 , \mathcal{Y}_1 , \ldots , \mathcal{Y}_n\right)$.
- (5) Il existe $a>2$ tel que presque sûrement \[\sup_{n>0}\E\left(\left|\mathcal{I}(v_1,\ldots, v_d,\mathcal{Y}_n)\right|^a|\mathcal{F}_{n-1}\right)<\infty.\]
-
$\displaystyle \lim_{N \to \infty}\frac{\beta_N}{\sum_{n=1}^N \gamma_n}=0$,
- $\displaystyle \lim_{N \to \infty}\frac{\sum_{n=1}^{N} \gamma_n c_n}{\sum_{n=1}^{N}\gamma_n}=0$,
- $\displaystyle\lim_{N \to \infty}\frac{\sum_{n=1}^{N} \frac{\gamma_n^2}{c_n^2\beta_{n-1}}}{\sum_{n=1}^{N} \gamma_n}=0$,
- $\displaystyle \sum_{n=1}^{+ \infty} \left(\frac{\gamma_n}{c_n}\right)^2<\infty$.