- 1. Introduction
- 2. Représentation par jeu du Chaos
- 3. Chaînes de Markov à mémoire variable
- 4. Marches aléatoires persistantes
- 5. Arbres aléatoires
Ce chapitre est une présentation des travaux
[133, 19, 23, 24, 21, 28].
Avant toute chose, je commence par une petite mise en garde sur les notations. Les notations $(X_n)$ et $(U_n)$ ne sont pas homogènes sur le chapitre. J'ai choisi de garder des notations cohérentes avec les articles auxquels je fais référence, ce qui induit des variations entre sections. La suite $(X_n)$ désignera tantôt une suite de lettres, tantôt une suite de points ou une suite de longueur de branches. La notation $(U_n)$ pourra correspondre à une suite de lettres indexée par $\Nset$ dans certaines sections, ou indexée par $\Zset$ dans d'autres. Ces notations sont toutes reprécisées en début de chaque section.
En théorie de l'information, une source stochastique est un mécanisme aléatoire qui émet, à chaque instant, un symbole choisi dans un alphabet fini. Le plus souvent en informatique, on se limite aux sources les plus simples : sources sans mémoire, où chaque symbole est produit indépendamment de
l'histoire, ou chaînes de Markov, où la production d'un symbole ne dépend que d'une partie
bornée de l'histoire. Une analyse plus réaliste des algorithmes (texte, recherche, tri) doit prendre en compte
des modèles de sources plus généraux, où la possible corrélation entre symboles émis est plus forte, avec une
portée plus étendue. Une chaîne de Markov à mémoire variable (VLMC, de l'anglais Variable Length Markov Chain) est une extension naturelle des chaînes de Markov. Ce modèle fournit un compromis intéressant: suffisamment général pour
pouvoir représenter des sources diverses, suffisamment structuré pour pouvoir être précisément étudié.
La première partie de ce chapitre résume un travail que j'ai effectué en thèse dans les articles [28, 133]. Il s'agit d'utiliser un mécanisme de représentation de séquences par jeu du Chaos pour caractériser l'ordre de dépendance d'une chaîne de Markov. La bijection entre les points de la représentation et l'historique de toute la séquence parcourue permet d'éviter les méthodes basées sur le comptage de mots. En d'autres termes, plutôt que de s'intéresser au processus décrivant la suite des lettres $(u_n)_{n\geq 1}$ le long d'une séquence, il peut s'avérer plus utile de s'intéresser à la suite des historiques $(U_n)_{n\geq 1}$ avec $U_n\egaldef u_1\ldots u_n$. Quel que soit l'ordre de dépendance Markovienne sur la suite $(u_n)_{n\geq 1}$, le processus $(U_n)_{n\geq 1}$ reste une chaîne de Markov d'ordre un.
On effectue ce même changement d'échelle lorsque l'on étudie les chaînes de Markov d'ordre variable dans la section 3. Plutôt que d'étudier directement la chaîne avec ses ordres de dépendance variables, on s'intéresse au processus contenant l'historique. Comme la dépendance peut être d'ordre infini, l'historique est un mot infini à gauche. La VLMC est aussi une chaîne de Markov d'ordre un sur l'ensemble des mots infinis à gauche. La section 3 définit le modèle VLMC et montre que ce processus peut être produit par une source dynamique explicite. Le formalisme des sources dynamiques introduit par [37] est rappelé dans la section 3.2.1.
Les deux dernières sections sont des études du comportement de structures aléatoires construites à partir de chaînes de Markov ou VLMC. Dans la section 4, l'objet d'étude est une marche aléatoire persistante, en dimension un, dont les incréments sont générés par une VLMC. La dernière partie contient des résultats asymptotiques sur le comportement d'arbres aléatoires de compression construits à partir de VLMC.
Le développement de la génétique et l'accélération des programmes de séquençage provoquent des besoins importants de représentation et de stockage de l'ADN. La Chaos Game Representation (CGR) est à la fois une méthode de représentation graphique et un outil de stockage. Cette méthode itérative fut appliquée pour la première fois aux séquences d'ADN par [75].
L'algorithme de représentation est défini de la façon suivante. Pour un alphabet fini $\CA$ constitué de $d$ lettres, pour un borélien borné $S\subset\Rset^q$, où $q$ est un entier positif, on définit la collection de fonctions affines $\{T_u, u\in
\CA\}$, liées à un facteur de contraction réel $\rho$ et à une famille $\{\ell_u, u\in
\CA\}$ d'éléments de $\Rset^q$ avec
$0<\rho<1$, par
À partir d'une suite de symboles dans un alphabet fini, la CGR associe une
trajectoire dans $S$. La définition de Jeffrey
est le cas particulier de la CGR obtenue en choisissant l'alphabet $\CA=\{A,C,G,T\}$ des nucléotides de l'ADN, $S=[0,1[^2$, $\rho=1/2$. De plus, les 4 lettres sont situées aux quatre sommets du carré unité, avec
\[
\ell_A=(0,0),\quad \ell_C=(0,1), \quad \ell_G=(1,1),\quad\ell_T=(1,0).
\]
La relation (3) s'écrit alors, pour $0\leq n \leq N-1$,
\[
X_{n+1}=\frac{1}{2}(X_n+\ell_{u_{n+1}}),
\]
avec $X_0=(\frac{1}{2},\frac{1}{2})$. La CGR peut bien entendu être définie sur d'autres ensembles que le carré.
La Figure Figure 1 illustre la
construction de la CGR pour le mot $ATGCGAGTGT$. On peut visualiser
sur la Figure Figure 2 deux exemples de CGR de séquences d'ADN de
longueur 70000.
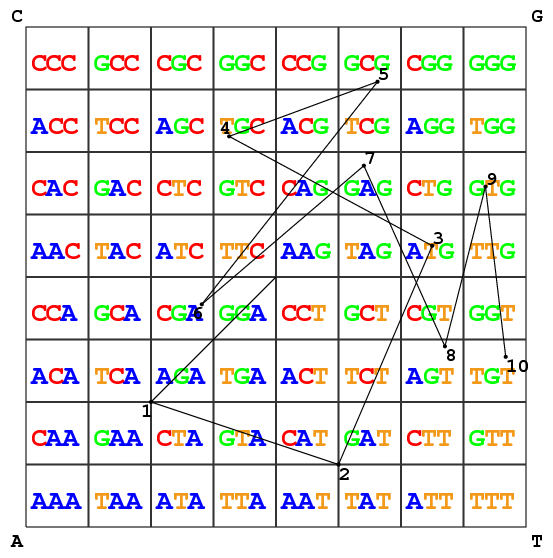
On associe au mot $w=u_{1}\ldots u_{n}$ l'ensemble $Sw$ défini par
La suite $(U_n)$ étant fixée, la CGR $(X_n)$ est elle aussi déterministe. Lorsque l'on met un modèle aléatoire sur la séquence d'ADN, la CGR devient elle aussi aléatoire de facto. Il est clair que la suite $(X_n)$ de points définissant la CGR forme une chaîne de
Markov d'ordre $1$, quel que soit le niveau de dépendance dans le mot aléatoire $U=u_1u_2\ldots$. En effet, tout le passé de la séquence à un instant donné $n$
peut être retrouvé à partir de la valeur de $X_{n}$: l'équation (3) entraîne, par construction, que $X_n\in Su_n$. On identifie ainsi $u_n$. A partir de la relation de récurrence (3): $X_{n-1}=\frac{X_n}{\rho}-\ell_{u_n}$. $X_{n-1}$ est donc déterminé à partir de
$X_{n}$, et on itère ainsi jusqu'au point initial $X_{0}$.
Ainsi, les tribus $\sigma\bigl(X_n\bigr)$ et $\sigma\bigl(X_0, (u_k)_{1\leq k \leq
n}\bigr)$ sont égales et
\[\sigma\bigl(X_n\bigr)=\sigma\bigl(X_1, \ldots X_n\bigr).\]
Conditionner par rapport au point $X_{n}$ équivaut à conditionner par rapport à tout le
passé. Travailler avec la suite $(X_n)$ revient donc à faire un changement d'échelle sur l'ordre de dépendance dans la suite observée. On utilise cette propriété pour caractériser la structure de dépendance.
J'ai proposé dans [133] une famille de tests asymptotiques permettant de déterminer l'ordre de dépendance d'une chaîne de Markov en utilisant la représentation CGR.
La correspondance bijective entre l'ensemble des séquences possibles et l'ensemble des points de
la CGR suggère de noter, pour un mot $w=v_1\ldots
v_m$ et pour un ensemble $B \subset S$,
Supposons maintenant que la suite de mots $(U_n)$ soit stationnaire et ergodique, et
notons $\pi$ la mesure limite invariante de sa CGR sur $S$. La propriété de $\pi$
énoncée ci-dessous permet de caractériser une suite sans mémoire.
On étend cette caractérisation au cas Markovien:
A partir des caractérisations précédentes, on construit un test de $H_0$ contre $H\setminus H_0$, puis de $H_m$ contre $H\setminus
H_m$. La notation $\hat\pi_{n}$ désigne la mesure
empirique associée à la CGR $(X_n)_{n\geq 0}$: pour tout ensemble $B$,
\[ \hat\pi_{n}(B)\egaldef \frac{1}{n}\sum_{j=1}^{n}\ind{X_j \in B}.\]
On définit la statistique $R_{n}$ inspirée par la propriété Propriété 2:
\[
R_n(B,w,u)
\egaldef \sqrt{n} \frac{\hat\pi_{n}(Sw)\hat\pi_{n}(Bwu)
-\hat\pi_{n}(Swu)\hat\pi_{n}(Bw)}
{\sqrt{\hat\pi_{n}(Sw)\hat\pi_n(Swu)\hat \pi_{n}(Bw)}}.
\]
De plus, $q_{\alpha}(d)$ désigne le $(1-\alpha)$-quantile de la loi de chi-deux $\chi^2(d)$.
- Pour une partition $\CP$ de $S$, avec $|\CP|=K>1$, l'ensemble
$
\Bigg\{\sum_{wu \in \CA^m \times\CA, \ B \in \CP} R_{n}^{2}(B,w,u) > q_{\alpha}\Bigl[d^m(d-1)(K-1)\Bigr]\Bigg\}
$(8)
est une région de rejet d'un test de niveau asymptotique $\alpha$, de $H_m$ contre $H\setminus H_m$.
- Sous $H\setminus H_m$, et en supposant qu'il existe $B \in \CP$ tel que $ \pi(Sw)\pi(Bwu)\neq\pi(Bw)\pi(Swu), $(9) le test construit à partir de la région de rejet (8) est asymptotiquement consistant.
Avec la même méthode, on peut construire des tests d'adéquation à une loi,
basés sur des statistiques analogues à celles utilisées pour les tests de
structure.
La preuve repose sur le théorème de la limite centrale pour martingales vectorielles et sur le théorème de Cochran. L'idée dans le cas de la caractérisation « sans mémoire » est de décomposer la différence
\[D_n(B,v)\egaldef \sqrt{n}\left(\hat\pi_n(Bv)-\hat\pi_n(B)\hat\pi_n(Sv)\right) \]
sous la forme
\[D_n(B,v)=\frac{1}{\sqrt{n}}M_n(B,v)\left(1+\eta_n\right),\]
avec
\[M_n(B,v)\egaldef \sum_{j=1}^n\ep_j(v)V_{j-1}(B), \quad \ep_j(v)\egaldef \ind{u_j=v}-\PP(u_j=v), \quad V_j(B)\egaldef \ind{B}(X_j)-\pi(B)\]
et où $(\eta_n)_n$ est une suite de variables aléatoires tendant en probabilités vers $0$. La suite $(M_n(B,v))$ est une martingale adaptée à la filtration naturelle $\sigma(X_n)$. Les propriétés bien connues pour les martingales permettent d'obtenir le théorème de test de caractérisation. L'idée est la même dans le cas de la caractérisation Markovienne, même si la décomposition demande un peu plus de minutie.
Pour éviter un choix rigide d'une partition unique, on peut proposer une
généralisation du test précédent à une collection de partitions de $S$. L'idée
est inspirée de la méthode de Bonferroni décrite dans [9]. Pour une
collection finie $\Pi~=~\{\CP_{1},\ldots \CP_{p}\}$, avec
$K_{j}\egaldef |\CP_{j}|$, $H_{m}$ est rejetée dès que l'une des partitions
$\CP_{j}$ la rejette, i.e.
\[Z_{(m)}\egaldef \sup_{1 \leq j \leq p}\Bigg\{\sum_{B \in \CP_{j}, v \in \CA} R_n^{2}(B,w,v)- q_{\alpha_{j}}\Bigl[d^m(d-1)(K_{j}-1)\Bigr]\Bigg\}>0.
\]
Il reste à choisir le niveau $\alpha_{j}$ de chaque partition $\CP_{j}$ pour
obtenir un niveau global égal à $\alpha$ pour la collection
$\Pi$, à l'aide d'une procédure bien définie.
En pratique, le choix de la partition est crucial. Deux partitions de même taille n'ont pas nécessairement le même
taux de rejet empirique. On constate à partir de simulations numériques que le taux de rejet de chaînes de Markov de
longue dépendance augmente lorsque le nombre d'ensembles constituant la
partition augmente. Les partitions les plus grosses sont souvent les plus robustes mais leur niveau converge plus lentement vers le niveau asymptotique. La puissance du test construit à partir d'une collection de partitions est
comparable à la puissance du meilleur des tests construits sur les partitions
elles-mêmes. En mélangeant plusieurs partitions, on peut même parfois améliorer la
performance du test. Considérer une collection peut être une
solution au problème crucial du choix d'une partition unique.
Les statistiques basées sur les points de la CGR sont plus générales que les statistiques des tests classiques basés sur le comptage de mots: ces tests classiques ne sont pas consistants contre toutes
les alternatives stationnaires ergodiques contrairement
aux tests basés sur la CGR. Pour illustrer ce point, on peut considérer la famille suivante
de chaînes de Markov mixées d'ordre $m>1$: dans un premier temps,
on génère $m$ chaînes de Markov indépendantes $U^{(1)},\ldots, U^{(m)}$
d'ordre $1$ comme ci-dessus; puis la séquence finale $U$ est obtenue par
l'agrégation
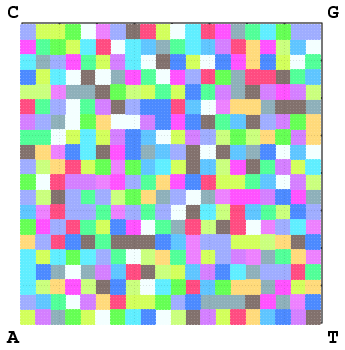
[44] utilisent la CGR pour caractériser et classifier les
espèces. Ils utilisent les fréquences d'apparition de tous les mots, qui forment alors
une « signature génomique ». En effet, une analyse de fréquences le long d'un
gène permet de mettre en évidence des similarités et des différences entre les
espèces. Dans leur étude, la CGR n'est qu'un outil permettant de
représenter ces signatures sous forme d'images, dans lesquelles les
zones les plus foncées correspondent aux
mots les plus fréquents. De plus, ils affirment
que cette spécificité de la signature génomique, qui permet de « caractériser le
style d'écriture », est une conséquence de l'action de l'environnement d'une part, et des structures de
contraintes d'autre part. La Figure 6 permet de visualiser plusieurs CGR pour des espèces différentes.
[76, 83] utilisent un profil de fréquences relatives
de dinucléotides comme signature génomique. Avec les notations de la Propriété 1, le rapport
d'abondance relative du dinucléotide $uv$ peut s'écrire sous la forme
Il m'a semblé naturel dans ce contexte d'étendre cette notion d'abondance relative de dinucléotides grâce à la CGR en faisant une partition de $S$ et en définissant un rapport d'abondance relative basé sur
la CGR par
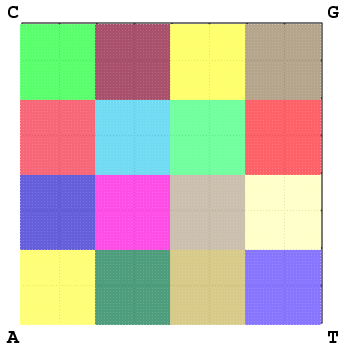
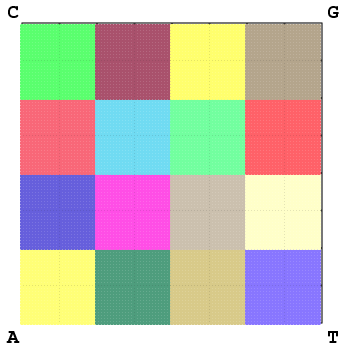
On construit alors une matrice de distances entre espèces à partir de ces rapports d'abondance et on constate, en comparant ces matrices de distances, que
l'utilisation de partitions qui ne correspondent pas à des mots, ni à des unions de
mots, permet un gain de précision et d'information dans la comparaison des
séquences biologiques ainsi que l'obtention de meilleurs arbres taxonomiques générés avec la méthode de clustering dite Neighbor-Joining (grâce à l'outil NJPLOT), comme l'illustrent les figures Figure 4 et Figure 5.
| Homo sapiens (chr. 4) |  |
Souris (chr. 2)  |
 |
Choléra  |
 |
Canis familiaris (chr. 11)  |
 |
Saccharomyces cerevisiae (chr. 4)  |
 |
Arabidopsis thaliana (chr. 1)  |
 |
Le gain d'information sur la structure de la séquence est obtenu en utilisant le changement d'échelle qu'est la CGR, où chaque point garde en mémoire l'historique de toute la séquence. Cette idée est à la base du formalisme que nous avons introduit pour définir l'objet de la section suivante: les chaînes de Markov à mémoire variable. Plutôt que de regarder le processus de succession des lettres avec une longueur de dépendance fonction du motif observé, nous avons redéfini les chaînes de Markov à mémoire variable comme une chaîne de Markov d'ordre un sur les mots contenant tout le passé, i.e les mots infinis « à gauche ».
Dans cette section, on modélise une suite, indexée par $\Zset$, de lettres dans un alphabet fini $\CA$. Comme pour la CGR où l'idée est de remplacer une suite de lettres de $\CA$ par une suite de variables contenant l'historique de toute la séquence et formant de ce fait une chaîne de Markov d'ordre $1$, il est naturel d'associer à une suite de lettres $(X_n)_{n\in\Zset}$ à valeur dans $\CA^\Zset$, un processus $(U_n)_{n\in \Nset}$ à valeur dans l'ensemble des mots infinis à gauche $\CL\egaldef \CA^{-\Nset}$ ($\CL$ pour left). A chaque étape on passe de $U_n = \dots X_{-1}X_0X_1 \dots X_n$ à $U_{n+1}$ en ajoutant une lettre $X_{n+1}$ à droite avec une évolution décrite par les probabilités de transition $\PP(U_{n+1} = U_n\alpha | U_n)$, pour $\alpha\in \CA$.
Dans le contexte des chaînes à proprement parler, jusqu'à présent le point de vue a surtout été d'ordre statistique depuis [67] qui parle de « chaîne d'ordre infini » (chains of infinite order) pour exprimer le fait que la production d'une nouvelle lettre dépend d'un nombre fini mais non borné de lettres précédentes.
[38] s'intéressent à des chaînes à mémoire infinie. [120] introduit une classe de modèles où la transition entre $U_n$ et $U_{n +1}$ dépend de $U_n$ au travers d'un suffixe fini de $U_n$ qu'il appelle contexte. Les contextes peuvent être stockés dans des feuilles d'un arbre appelé arbre des contextes. Ainsi le modèle est entièrement défini par une famille de distributions de probabilités indexées par les feuilles d'un arbre de contexte. Le nom Variable Length Markov Chain (VLMC) est dû à [18]. On trouve dans [58] une bibliographie plus complète sur le sujet.
On commence par définir un arbre des contextes probabilisé; on lui associe ensuite une chaîne de Markov à mémoire variable (VLMC).
Pour simplifier les notations, on se place dans le cas particulier d'un alphabet de deux lettres $\CA = \{ 0,1\}$ mais la définition s'étend à n'importe quel alphabet fini. On note $\CW$ l'ensemble de tous les mots sur $\CA$.
On note également $\mathcal{R}\egaldef \CA^{\Nset}$ l'ensemble des mots infinis à droite ($\mathcal{R}$ pour right). Pour un entier $k$ et un mot $w=\alpha _{-k}\cdots \alpha _0$, $\overline w$ désigne le mot retourné \[\overline w \egaldef \alpha_0\cdots\alpha_{-k}.\]
Le cylindre basé sur $w$ est l'ensemble des mots infinis à gauche ayant pour suffixe $w$:
\[\CL w\egaldef \{ s\in\CL,~\forall j\in\{ -k,\cdots ,0\},~s_j=\alpha _j\}.\]
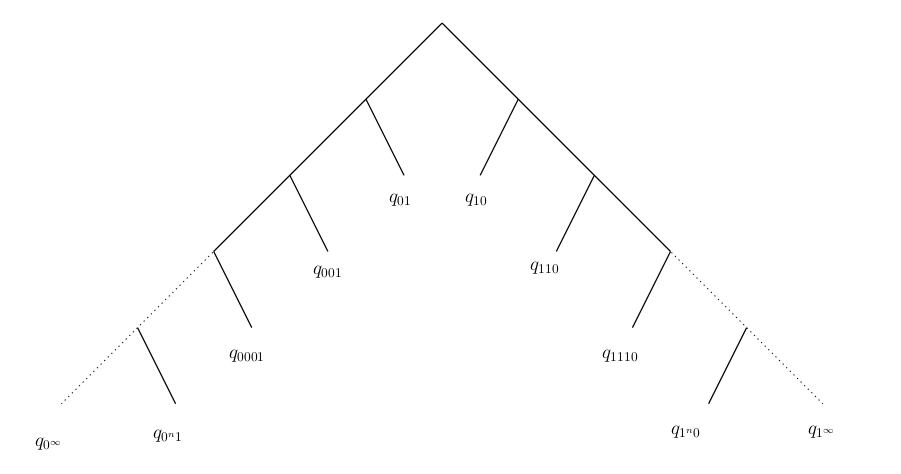
On considère un arbre planaire enraciné $\CT$ et on définit l'ensemble de ses feuilles $\CC(\CT)$ comme étant la réunion de l'ensemble des feuilles finies $\{ u\in \CT, \forall j\in\CA, uj\notin \CT\}$ et de l'ensemble des feuilles infinies $\{u\in\mathcal{R}, \forall v \hbox{ préfixe de } u, v\in \CT\}$. Les nœuds internes sont les éléments du complémentaire, dans l'arbre $\CT$, de toutes les feuilles.
Sur la Figure 7 on trouve un exemple d'arbre des contextes probabilisé fini avec $5$ contextes.
![\begin{tikzpicture}
\pgfsetlinewidth{1bp}
\pgfsetcolor{black}
\draw [] (109.5bp,230.53bp) .. controls (105.66bp,221.59bp) and (95.209bp,197.32bp) .. (87.841bp,180.21bp);
\draw [] (112.5bp,230.53bp) .. controls (117.72bp,218.39bp) and (135.13bp,177.95bp) .. (140.45bp,165.61bp);
\draw [] (140.41bp,158.53bp) .. controls (134.85bp,146.39bp) and (116.31bp,105.95bp) .. (110.65bp,93.607bp);
\draw [] (143.59bp,158.53bp) .. controls (147.69bp,149.59bp) and (158.81bp,125.32bp) .. (166.65bp,108.21bp);
\draw [] (106.46bp,86.906bp) .. controls (99.407bp,78.293bp) and (79.115bp,53.53bp) .. (64.888bp,36.169bp);
\draw [] (110.92bp,86.859bp) .. controls (113.2bp,83.2bp) and (117.17bp,77.015bp) .. (121bp,72bp) .. controls (130.5bp,59.553bp) and (142.04bp,46.277bp) .. (151.3bp,36.004bp);
\draw [] (140.73bp,288.55bp) .. controls (144.24bp,281.52bp) and (152.43bp,265.14bp) .. (158.92bp,252.15bp);
\draw [] (137.33bp,288.55bp) .. controls (132.34bp,278.21bp) and (117.56bp,247.58bp) .. (112.62bp,237.36bp);
\begin{scope}
\definecolor{strokecol}{rgb}{0.0,0.0,0.0};
\pgfsetstrokecolor{strokecol}
\draw (175bp,90bp) node {$q_{011}$};
\end{scope}
\begin{scope}
\definecolor{strokecol}{rgb}{0.0,0.0,0.0};
\pgfsetstrokecolor{strokecol}
\definecolor{fillcol}{rgb}{0.0,0.0,0.0};
\pgfsetfillcolor{fillcol}
\filldraw [opacity=1.0] (139bp,292bp) ellipse (4bp and 4bp);
\end{scope}
\begin{scope}
\definecolor{strokecol}{rgb}{0.0,0.0,0.0};
\pgfsetstrokecolor{strokecol}
\draw (50bp,18bp) node {$q_{0100}$};
\end{scope}
\begin{scope}
\definecolor{strokecol}{rgb}{0.0,0.0,0.0};
\pgfsetstrokecolor{strokecol}
\draw (168bp,18bp) node {$q_{0101}$};
\end{scope}
\begin{scope}
\definecolor{strokecol}{rgb}{0.0,0.0,0.0};
\pgfsetstrokecolor{strokecol}
\definecolor{fillcol}{rgb}{0.0,0.0,0.0};
\pgfsetfillcolor{fillcol}
\filldraw [opacity=1.0] (109bp,90bp) ellipse (4bp and 4bp);
\end{scope}
\begin{scope}
\definecolor{strokecol}{rgb}{0.0,0.0,0.0};
\pgfsetstrokecolor{strokecol}
\definecolor{fillcol}{rgb}{0.0,0.0,0.0};
\pgfsetfillcolor{fillcol}
\filldraw [opacity=1.0] (111bp,234bp) ellipse (4bp and 4bp);
\end{scope}
\begin{scope}
\definecolor{strokecol}{rgb}{0.0,0.0,0.0};
\pgfsetstrokecolor{strokecol}
\draw (168bp,234bp) node {$q_{1}$};
\end{scope}
\begin{scope}
\definecolor{strokecol}{rgb}{0.0,0.0,0.0};
\pgfsetstrokecolor{strokecol}
\definecolor{fillcol}{rgb}{0.0,0.0,0.0};
\pgfsetfillcolor{fillcol}
\filldraw [opacity=1.0] (142bp,162bp) ellipse (4bp and 4bp);
\end{scope}
\begin{scope}
\definecolor{strokecol}{rgb}{0.0,0.0,0.0};
\pgfsetstrokecolor{strokecol}
\draw (80bp,162bp) node {$q_{00}$};
\end{scope}
\end{tikzpicture}](http://cenac.perso.math.cnrs.fr/hdr/_latex2.svg "\begin{tikzpicture}
\pgfsetlinewidth{1bp}
\pgfsetcolor{black}
\draw [] (109.5bp,230.53bp) .. controls (105.66bp,221.59bp) and (95.209bp,197.32bp) .. (87.841bp,180.21bp);
\draw [] (112.5bp,230.53bp) .. controls (117.72bp,218.39bp) and (135.13bp,177.95bp) .. (140.45bp,165.61bp);
\draw [] (140.41bp,158.53bp) .. controls (134.85bp,146.39bp) and (116.31bp,105.95bp) .. (110.65bp,93.607bp);
\draw [] (143.59bp,158.53bp) .. controls (147.69bp,149.59bp) and (158.81bp,125.32bp) .. (166.65bp,108.21bp);
\draw [] (106.46bp,86.906bp) .. controls (99.407bp,78.293bp) and (79.115bp,53.53bp) .. (64.888bp,36.169bp);
\draw [] (110.92bp,86.859bp) .. controls (113.2bp,83.2bp) and (117.17bp,77.015bp) .. (121bp,72bp) .. controls (130.5bp,59.553bp) and (142.04bp,46.277bp) .. (151.3bp,36.004bp);
\draw [] (140.73bp,288.55bp) .. controls (144.24bp,281.52bp) and (152.43bp,265.14bp) .. (158.92bp,252.15bp);
\draw [] (137.33bp,288.55bp) .. controls (132.34bp,278.21bp) and (117.56bp,247.58bp) .. (112.62bp,237.36bp);
\begin{scope}
\definecolor{strokecol}{rgb}{0.0,0.0,0.0};
\pgfsetstrokecolor{strokecol}
\draw (175bp,90bp) node {$q_{011}$};
\end{scope}
\begin{scope}
\definecolor{strokecol}{rgb}{0.0,0.0,0.0};
\pgfsetstrokecolor{strokecol}
\definecolor{fillcol}{rgb}{0.0,0.0,0.0};
\pgfsetfillcolor{fillcol}
\filldraw [opacity=1.0] (139bp,292bp) ellipse (4bp and 4bp);
\end{scope}
\begin{scope}
\definecolor{strokecol}{rgb}{0.0,0.0,0.0};
\pgfsetstrokecolor{strokecol}
\draw (50bp,18bp) node {$q_{0100}$};
\end{scope}
\begin{scope}
\definecolor{strokecol}{rgb}{0.0,0.0,0.0};
\pgfsetstrokecolor{strokecol}
\draw (168bp,18bp) node {$q_{0101}$};
\end{scope}
\begin{scope}
\definecolor{strokecol}{rgb}{0.0,0.0,0.0};
\pgfsetstrokecolor{strokecol}
\definecolor{fillcol}{rgb}{0.0,0.0,0.0};
\pgfsetfillcolor{fillcol}
\filldraw [opacity=1.0] (109bp,90bp) ellipse (4bp and 4bp);
\end{scope}
\begin{scope}
\definecolor{strokecol}{rgb}{0.0,0.0,0.0};
\pgfsetstrokecolor{strokecol}
\definecolor{fillcol}{rgb}{0.0,0.0,0.0};
\pgfsetfillcolor{fillcol}
\filldraw [opacity=1.0] (111bp,234bp) ellipse (4bp and 4bp);
\end{scope}
\begin{scope}
\definecolor{strokecol}{rgb}{0.0,0.0,0.0};
\pgfsetstrokecolor{strokecol}
\draw (168bp,234bp) node {$q_{1}$};
\end{scope}
\begin{scope}
\definecolor{strokecol}{rgb}{0.0,0.0,0.0};
\pgfsetstrokecolor{strokecol}
\definecolor{fillcol}{rgb}{0.0,0.0,0.0};
\pgfsetfillcolor{fillcol}
\filldraw [opacity=1.0] (142bp,162bp) ellipse (4bp and 4bp);
\end{scope}
\begin{scope}
\definecolor{strokecol}{rgb}{0.0,0.0,0.0};
\pgfsetstrokecolor{strokecol}
\draw (80bp,162bp) node {$q_{00}$};
\end{scope}
\end{tikzpicture}")
- aucun mot de $\mathcal{K}$ n'est un préfixe d'un autre mot de $\mathcal{K}$
- $\forall r\in \mathcal{R}$, $\exists u\in \mathcal{K}$, $u$ est un préfixe de $r$.
Autrement dit pour les mots infinis à gauche, on a
- si $\overline{w}\in \CT$ alors $\lpref(w)=\overline{w}$;
- si $\overline{w}\in \CW \setminus \CT$ alors $\lpref(w)$ est l'unique contexte $\alpha_1\dots\alpha_N$ tel que $w$ ait $\alpha_N\dots\alpha_1$ comme suffixe.
On suppose maintenant qu'il existe une mesure stationnaire $\pi$ sur $\CL$ et on considère la VLMC en mode stationnaire (de loi $\pi$). Pour alléger les notations, pour un mot $w\in\CW$, on écrit $\pi(w)$ plutôt que $\pi(\CL w)$: $\pi(w)=\PP(U_0 \in \CL w)=\PP(X_{-(|w|-1)}\ldots X_0=w)$.
Lorsque $u$ est un nœud interne de l'arbre des contextes, on étend la notation $q_{u}$ de la façon suivante: pour tout $\alpha\in\CA$,
- pour tout mot fini $w\in\CW$ et toute lettre $\alpha\in\CA$, $ \pi (w\alpha )=\pi (w)q_{\petitlpref (w)}(\alpha ); $(16)
- pour tout mot fini $w=\alpha _1\dots\alpha _N\in\CW$, $ \pi (w)=\prod _{k=0}^{N-1}q_{\petitlpref (\alpha _1\dots \alpha _k)}(\alpha _{k+1}) $(17) (si $k=0$, $\alpha _1\dots \alpha _k$ désigne le mot vide $\emptyset$, $\lpref(\emptyset) = \emptyset$, $q_{\emptyset}(\alpha)=\pi(\alpha)$ et $\pi(\emptyset) = \pi(\CL) = 1$).
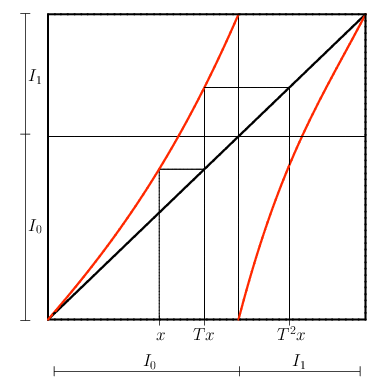
Dans cette section, nous établissons le lien entre le point de vue « chaîne stochastique » de la chaîne de Markov à mémoire variable $(U_n)$ et le point de vue source au sens de la théorie de l'information. Ici $I$ désigne l'intervalle $[0,1]$ et la mesure de Lebesgue d'un Borélien $J$ est notée $|J|$.
On présente ici le formalisme classique des sources dynamiques probabilisées définies dans [37]). Une telle source est définie par quatre éléments:
- une partition topologique de $I$ en intervalles $(I_\alpha)_{\alpha \in \CA}$,
- une fonction de codage $\rho : I \to \CA$, telle que, pour toute lettre $\alpha$, la restriction de $\rho$ à $I_{\alpha}$ est égale à $\alpha$,
- une application $T: I\to I$,
- une mesure de probabilité $\mu$ sur $I$.
Pour un mot fini $w=\alpha _0\dots\alpha _N\in\CW$, on note $B_w$
l'ensemble des réels $x$ telle que la suite $(Y_n)_{n\in\Nset}$ ait $w$ comme préfixe. La probabilité qu'une source émette un symbole commençant par $w$ est égale à $\mu(B_w)$. Lorsque la mesure initiale $\mu$ sur $I$ est $T$-invariante, la source dynamique génère un processus aléatoire stationnaire à valeurs dans $\CA$.
Soit $(U_n)_{n\geq 0}$ une VLMC stationnaire définie par l'arbre des contextes probabilisé $(\CT,(q_c)_{c\in\CC})$ et de probabilité stationnaire $\pi$ sur $\CL$.
On commence par construire l'unique subdivision $\CA$-adique $(I_w)_{w\in\CW}$ de $I$ associée à $\pi$ définie par $\forall w\in\CW,~|I_w|=\pi (\overline w).$
On considère alors les trois partitions topologiques ordonnées suivantes:
- la partition de codage $I=I_0+I_1$.
- la partition verticale résultant de la propriété de cutset de l'ensemble des contextes: \[I=\ordPart{c\in\CC}I_c.\]
- la partition horizontale \[I=\ordPart{\alpha\in\CA, c\in\CC}I_{\alpha c}.\]
- la restriction de $T$ à tout intervalle $I_{\alpha c}$ est affine et croissante;
- pour tout $(\alpha,c) \in\CA\times \CC$, $T(I_{\alpha c})=I_c$.
On construit maintenant la source dynamique probabilisée $\left((I_\alpha )_{\alpha\in\CA},\rho ,T, |.|\right)$ construite à partir d'une VLMC stationnaire. Elle fournit un processus aléatoire $(Y_n)_{n\in\Nset}$ à valeurs dans $\CA$ défini par $Y_n\egaldef\rho(T^n\xi )$, où $\xi$ est une variable aléatoire de loi uniforme sur $I$. Comme la mesure de Lebesgue est invariante par $T$ par construction, toutes les variables aléatoires $Y_n$ ont la même loi et $\PP (Y_n=0)=|I_0|=\pi (0)$.
- la mesure de Lebesgue est invariante par $T$.
- si $\xi$ est une variable aléatoire de loi uniforme sur $I$, les processus $(X_n)_{n\in\Nset}$ et $(\rho(T^n\xi ))_{n\in\Nset}$ sont symétriquement distribués.
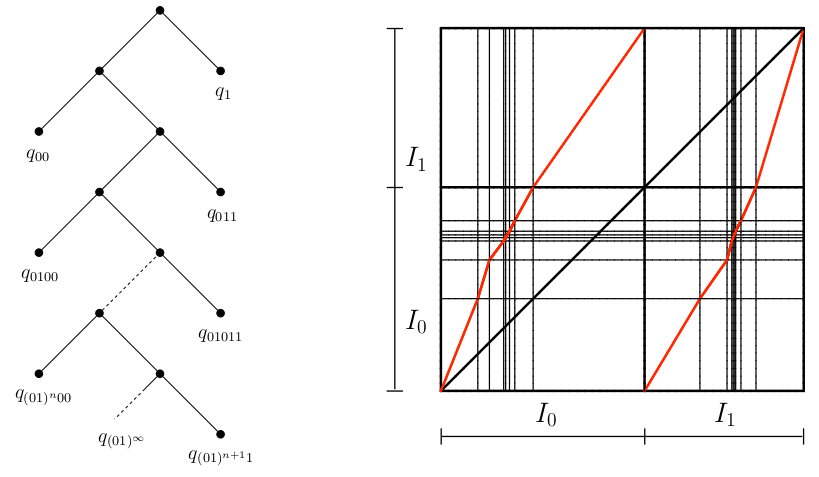
Le peigne est un cas particulier d'arbre des contextes possédant une unique branche infinie. De ce fait, le processus des lettres $(X_n)$ de la VLMC n'est a priori pas Markovien. Plus précisément, on considère l'arbre des contextes dessiné sur la partie gauche de la Figure 9.
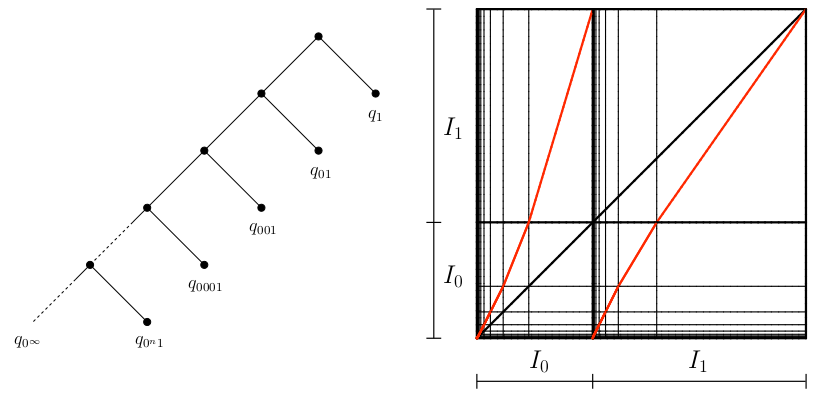
Pour le peigne, il y a une unique feuille infinie $0^\infty$ et toutes les feuilles finies sont de la forme $0^n1$, pour $n\in\Nset$.
Les données correspondant à cette VLMC sont donc les mesures de probabilité sur $\CA=\{ 0,1\}$: $q_{0^\infty}$ et $q_{0^n1},~n\in\Nset.$
- Cas irréductible: on suppose que $q_{0^\infty}(0)\neq 1$.
- Existence
Le processus Markovien $(U_n)_{n\geq 0}$ admet une mesure de probabilité invariante sur $\CL$ si et seulement si $\sum c_n$ converge, où $c_n$ est définie par $ c_n=\prod _{k=0}^{n-1}q_{0^k1}(0), \mbox{ pour }n\geq 1, \qquad \mbox{et} \quad c_0=1. $(18) - Unicité
On suppose que $\sum c_n$ converge et on note $S(1)\egaldef\sum _{n\geq 0}c_n.$ Alors la mesure invariante $\pi$ est unique et caractérisée par les formules (17) et $\pi (1)=\frac 1{S(1)}$. On obtient les probabilités des contextes et des nœuds internes: $ \pi (10^n)=\pi (1)c_n, \qquad \pi (0^n)=1-\pi (1)\sum _{k=0}^{n-1}c_k \quad \mbox{pour }n\geq 0. $(19) De plus, $\pi$ est triviale si et seulement si $q_1(0)=0$, en quel cas $\pi (1^\infty )=1$.
- Cas réductible: on suppose que $q_{0^\infty}(0)=1$.
- si $\sum c_n$ diverge, alors la mesure de probabilité triviale $\pi$ sur $\CL$ définie par $\pi (0^\infty )=1$ est l'unique mesure de probabilité invariante.
- Si $\sum c_n$ converge, alors il existe une famille de mesures invariantes à paramètre sur $\CL$. Plus précisément, pour $a\in [0,1]$, il existe une unique mesure de probabilités invariante $\pi _a$ sur $\CL$ telle que $\pi _a(0^\infty)=a$. La loi $\pi _a$ est caractérisée par $\pi _a(1)=\frac {1-a}{S(1)}$ et les formules (17) et (19). De plus, $\pi _a$ n'est pas triviale sauf sans les cas suivants:
- $a=1$ en quel cas $\pi _1$ est définie par $\pi _1(0^\infty )=1$;
- $a=0$ et $q_1(0)=0$, en quel cas $\pi _0$ est définie par $\pi _0(1^\infty )=1$.
La partition verticale est constituée des intervalles $I_{0^{n}1}$ pour $n\geq 0$, la partition horizontale des intervalles $I_{00^{n}1}$ et $I_{10^{n}1}$, pour $n\geq 0$, ainsi que deux intervalles provenant des contextes infinis $I_{0^{\infty}}$ et $I_{10^{\infty}}$. Dans le cas irréducible, $\pi(0^{\infty})=0$ et les deux intervalles $I_{0^{\infty}}$ et $I_{10^{\infty}}$ viennent des points d'accumulation de la partition en $0$ et $\pi(0)$.
Le comportement du temps d'entrée dans les cylindres est une question naturelle dans les systèmes dynamiques. Il existe une abondante littérature sur les propriétés asymptotiques de ces moments d'entrée pour différents types de systèmes (voir [1] pour une étude approfondie sur le sujet). La plupart des résultats utilise une approximation de la loi du temps d'entrée dans un petit cylindre par une loi exponentielle. Les résultats présentés dans ce paragraphe (issus de [23]) sont des résultats non asymptotiques.
Pour les suites indépendantes et identiquement distribuées, [15] fournissent la fonction génératrice de la première occurrence d'un mot. Ce résultat est étendu aux chaînes de Markov par [41]. Leurs travaux sont basés sur une relation de récurrence sur les probabilités d'occurrence de motifs. D'autres approches sont envisagées dans la littérature: l'une des techniques plus générales est la méthode dite de plongement Markovien introduite par [53] et développée ensuite dans [54], [85]. Il existe aussi une approche alternative avec des martingales (voir [61], [96], [143]). Ces deux approches sont comparées dans [118].
On considère le processus $X=(X_n)_{n \geq 0}$ des dernières lettres de $(U_n)_{n\geq 0}$, dans le cas particulier d'une VLMC stationnaire définie par un peigne infini. Soit $w=w_1 \ldots w_k$ un mot de longueur $k\geq 1$. On dit qu'on a une occurrence de $w$ en $n \geq k$ dans le mot infini $X$ si le mot $w$ se termine à la position $n$:
\[\{w \mbox{ en }n\}=\{X_{n-k+1}\ldots X_{n}=w\}=\{U_n \in \CL w\}.\]
Notons $T_w^{(r)}$ la position de la $r$ ème occurrence de $w$ dans $X$ et $\Phi_w^{(r)}$ sa fonction génératrice:
\[
\Phi_w^{(r)} (x) \egaldef \sum_{n\geq 0} \PP\left( T_w^{(r)} =n\right) x^n.
\]
Enfin, on utilise la notation suivante: pour tout mot fini $u$, pour tout contexte $c \in\CC$ et $n\geq 0$,
\[q_c^{(n)}(u)\egaldef \PP\left(X_{n-|u|+1}\ldots X_{n}=u|X_{-(|c|-1)}\ldots X_{0}=\overline c\right).\]
| $ S_w(x)$ | $=$ | $ C_w(x) + \sum_{j=k}^{\infty}q_{\petitlpref(w)}^{(j)}(w)x^j,$ |
| $ C_w(x)$ | $=$ | $ 1+\sum_{j=1}^{k-1}\ind{w_{j+1}\ldots w_{k}=w_{1}\ldots w_{k-j}}q_{\petitlpref(w)}^{(j)}\left(w_{k-j+1} \ldots w_k\right)x^j.$ |
Pour une suite stationnaire $(U_n)_{n\geqslant 0}$ de mesure invariante $\pi$, on cherche à mesurer l'indépendance entre deux mots $A$ et $B$ séparés de $n$ lettres. Pour $0\leqslant m\leqslant +\infty$, on note ${\cal F}_0^m$ la tribu engendrée par les $\{U_k , 0\leqslant k \leqslant m\}$ et on considère les mots $A\in{\cal F}_0^m$ et $B\in{\cal F}_0^{\infty}$. On s'intéresse en particulier au coefficient de mélange
Dans l'article [24], nous établissons l'expression exacte de $\psi(n,A,B)$ pour un peigne général. Par souci de concision, je choisis de ne présenter ici le résultat de ce calcul que pour deux exemples: l'un fournissant une suite $(U_n)$ $\psi$-mélangeante et l'autre une suite $(U_n)$ qui n'est pas uniformément mélangeante.
Le peigne logarithmique est défini par $c_0=1$ et pour $n\geqslant 1$ par
\[c_n = \frac{1}{n(n+1)(n+2)(n+3)}. \]
Les probabilités conditionnelles correspondantes sur les feuilles de l'arbre sont donc $q_1(0)=\frac{1}{24}$ et pour $n\geqslant 1$, $q_{0^n1}(0)=1-\frac{4}{n+4}.$
Le peigne factoriel est défini par les probabilités conditionnelles sur les feuilles $q_{0^n1}(0)= \frac 1{n+2}$ pour $n\geqslant 0$. Par conséquent on a
\[
c_n = \frac 1{(n+1)!}.
\]
On a obtenu dans [23] des résultats analogues (existence et unicité de mesure stationnaire, fonctions génératrices des instants d'occurrences de mots, séries de Dirichlet, système dynamique) pour un autre exemple de VLMC: le bambou. Ce modèle est défini par l'arbre des contextes probabilisé donné par la partie gauche de la Figure 10.
J'ai choisi de ne pas présenter le détail de ces résultats et de me limiter au cas du peigne. Sur le fond, le traitement du bambou a des analogies avec celui du peigne, car il possède également une propriété de renouvellement induit par les motifs $11$ ou $00$.
Les marches aléatoires classiques sont définies par
Avec un bon changement d'échelle pour la marche et un passage à la limite au cas continu, il est possible d'obtenir un mouvement brownien standard. Lorsque les incréments forment une chaîne de Markov d'ordre $1$, une courte mémoire est introduite dans la dynamique de la marche aléatoire: le processus est dit persistant ou est encore appelé marche aléatoire corrélée ou marche de Kac (voir [148, 150, 153, 152]). La marche n'est plus Markovienne dans ce cas et par un changement d'échelle adéquat, le processus renormalisé converge vers le processus du télégraphe intégré ([68, 130] et [131].
Dans l'article [19], nous généralisons ce résultat à une famille de marches aléatoires construites à partir d'incréments $(X_n)_{n\in\mathbb{N}}$ constituant une chaîne à mémoire variable. Plus précisément, pour une VLMC donnée $(U_n)_{n\geqslant 0}$, on définit $X_n$ comme étant la dernière lettre de $U_n$ pour $n\geq 0$. Lorsque $(X_n)_{n\in\mathbb{N}}$ est une chaîne de Markov d'ordre fini, il est naturel de penser que le processus limite sera très proche du télégraphe intégré. C'est pourquoi nous avons construit des chaînes à mémoire infinie afin d'identifier éventuellement un autre processus limite. La marche associée $(S_t)$ définie par (21) n'est pas Markovienne, elle est en quelque sorte très persistante. Cette marche est-elle de même nature que dans le cas Markovien d'ordre un ? La marche renormalisée par le bon changement d'échelle conduit-elle à un processus analogue à celui du télégraphe intégré ?
La chaîne de Markov à mémoire variable et non bornée que l'on considère dans cette section et que nous appellerons double peigne est définie de la façon suivante. On considère l'arbre des contextes donné sur la Figure 11.
On effectue maintenant un changement de codage: '0' est codé en '-1'. La suite des lettres $(X_n)$ de $(U_n)$ est donc dans à valeur dans l'alphabet $\{-1,1\}$.
La loi exacte de la marche aléatoire très persistante $(S_n)$ est donnée dans [19]. Son expression est assez compliquée et peut être simplifiée en s'intéressant à la fonction génératrice de la variable $S_{\tau+1}$, où $\tau$ est une variable de loi géométrique indépendante de la source $(U_n)$.
Une autre façon de comparer le processus $(S_n)$ avec celui de la marche aléatoire « classique » est d'analyser les fluctuations à l'infini.
- La suite $\displaystyle \frac{S_n}{n}$ converge p.s. et dans $L^1$ vers $\displaystyle\frac{\Theta_2-\Theta_1}{\Theta_1+\Theta_2}$ quand $n\to\infty$.
- De plus, si $ \sum_{n\ge 1}n\prod_{k=1}^{n-1}q_{0^n1}(0)<\infty \quad \mbox{et}\quad \sum_{n\ge 1}n\prod_{k=1}^{n-1}q_{1^n0}(1)<\infty, $(22) alors on a le théorème de la limite centrale: $ \frac{1}{\sqrt{n} \Upsilon}\left(S_n- n\frac{\Theta_2-\Theta_1}{\Theta_1+\Theta_2} \right)\cvl \CN\left(0,1\right), $(23) où la constante $\Upsilon$ est définie par $ \Upsilon=\frac{4}{\Theta_1+\Theta_2}\ \mathbb{E}\left[\left( T_1-\frac{\Theta_2 T_2}{\Theta_1+\Theta_2} \right)^2\right]. $(24)
On introduit un paramètre d'échelle $\ep>0$ ainsi que deux fonctions $f_1,f_2:[0,\infty[\to\mathbb{R}$ positives et continues à droite. On s'intéresse à la VLMC du double peigne (codée dans l'alphabet $\{-1,1\}$) définie par les probabilités de transition
| $ q_{(-1)^k1}(1)$ | $=$ | $f_1(k\ep)\ep+o(\ep),$(26) |
| $ q_{1^k(-1)}(-1)$ | $=$ | $f_2(k\ep)\ep+o(\ep).$(27) |
On associe à cette VLMC la marche construite à partir de ces incréments, que l'on note $(S_n^{\ep})$. Le processus $(S^{\ep}(t), t\geq 0)$ est linéaire par morceaux et satisfait, pour tout $n\in\mathbb{N}$,
| $ \mathbb{P}(\xi_{2n+1}-\xi_{2n}\ge t)=\exp\left(-\int_0^t f_2(u)\, du\right)$ |
| $ \mathbb{P}(\xi_{2n+2}-\xi_{2n+1}\ge t)=\exp\left(-\int_0^t f_1(u)\, du\right)$ |
Le processus $(S^{\ep}(t), t\geq 0)$ converge en loi (avec la topologie de Skorohod) lorsque $\ep\to 0$ vers $(S^0(t), t\geq 0)$.
Dans la dernière partie de ce chapitre, on s'intéresse à une autre famille d'objets construits à partir de certaines sources dynamiques: des arbres digitaux de compression de données.
Une propriété fondamentale de la CGR est que tous les mots possédant un même suffixe $w=w_1\ldots w_k$ sont regroupés dans une même zone $Sw$. À partir d'un mot $m=a_1a_2\ldots$ à valeur dans $\CA^{\Nset}$, on regroupe ainsi dans $Sw$ tous les points $X_n$ de la CGR tels que $a_{n-k+1}\dots a_{n-1}a_{n} = w$. Une idée naturelle est de « ranger » ces sous-séquences dans les nœuds
d'un arbre, tout en conservant la visualisation de répétitions de suffixes.
On supposera les lettres classées arbitrairement dans l'ordre $(A, C, G, T)$. On note $\CT$
l'arbre quaternaire infini complet. À chaque étape de la construction,
on insère un nœud dans $\CT$. On construit ainsi une suite de sous-arbres finis
$\CT_{n}$ de $\CT$, tous emboîtés $\CT_{1} \subset \CT_{2} \ldots \CT_{n}
\subset \ldots \subset \CT$.
Chaque sous-arbre $\CT_{n}$ possède $n$ nœuds étiquetés (sans compter la
racine). Étant donné un mot aléatoire
$m=a_{1}a_{2}\ldots$, l'arbre-CGR pousse en insérant successivement
des mots $a_{1}\ldots a_{i}$ dans l'arbre infini complet. Chaque nœud de
cet arbre possède $4$ branches correspondant au quadruplet ordonné $(A, C, G, T)$.
Tout d'abord, la lettre $a_{1}$ est insérée dans l'arbre infini
complet au niveau 1, juste sous la racine, sous la branche correspondant à
$a_1$. L'insertion du mot $a_{1} \ldots a_{n}$ est faite récursivement: on essaye tout d'abord de l'insérer au niveau 1
dans la branche correspondant à la dernière lettre rencontrée dans la lecture
de ce mot, c'est-à-dire $a_{n}$; si ce nœud est déjà
occupé, on essaye de l'insérer au niveau 2 de l'arbre dans le sous-arbre correspondant
à $a_{n}$, sous la branche correspondant à la lettre $a_{n-1}$. On répète
l'opération jusqu'au premier nœud non occupé au niveau $k$ dans la branche
correspondant à la lettre $a_{n-k+1}$; le mot $a_1\dots a_n$ est alors inséré
sur ce nœud. Si $k<n$, seul compte le suffixe $a_{n-k+1} \ldots a_{n}$ du
mot $a_1\dots a_n$ que l'on insère. On remarque que comme pour le processus de construction d'une VLMC, on analyse le préfixe retourné du mot parcouru.
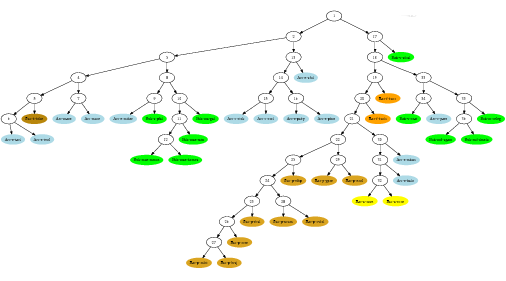
La Figure Figure 12 montre les premières étapes de la construction
de l'arbre-CGR correspondant à tout mot $m$ qui commence par
$w=GAGCACAGTGGAAGGG$. Chaque nœud est
étiqueté par son ordre d'insertion par souci de lisibilité.
GAGCACAGTGGAAGGG
GAGCACAGTGGAAGGG
GAGCACAGTGGAAGGG
GAGCACAGTGGAAGGG
GAGCACAGTGGAAGGG
Cette construction est motivée par la volonté de mesurer des
quantités statistiques révélées par la forme de l'arbre, afin de dégager de
nouvelles caractéristiques pour une loi de génération fixée.
L'arbre-CGR d'un mot aléatoire $m=a_{1}a_{2}\ldots$ est un arbre digital
de recherche (DST, de l'anglais Digital Search Tree)
obtenu par l'insertion successive dans un arbre quaternaire des
préfixes retournés du mot $m$:
| $ m(1)$ | $=$ | $a_{1}, \nonumber$(30) |
| $ m(2)$ | $=$ | $a_{2}a_{1}, \nonumber$ |
| $\vdots$ | $ \nonumber$ | |
| $ m(n)$ | $=$ | $a_{n}a_{n-1}\ldots a_{1},$ |
| $\vdots$ | $\nonumber$ |
Les mots insérés sont donc fortement dépendants,
contrairement aux DST classiques où les mots insérés sont indépendants
les uns des autres. Plusieurs résultats sont connus (voir chap. 6 dans [100]) sur la
hauteur, la profondeur d'insertion et le profil, pour des DST construits sur des
suites de mots indépendants, tous de même loi. Dans [21], nous nous intéressons aux propriétés asymptotiques de l'arbre-CGR, construit à partir de chaînes de Markov. En particulier, nous démontrons un résultat de convergence presque sûre pour les longueurs des
branches, ainsi qu'une propriété de convergence en probabilité pour la profondeur d'insertion. Comme pour d'autres arbres de compression classiques (voir [49] pour les tries et [45] pour les arbres binaires
de recherche), la différence de comportement asymptotique entre les DST classiques et les arbres-CGR, issus de séquences Markoviennes n'est pas visible au 1er ordre.
Dans le cas où les mots à insérer sont indépendants, mais à
valeurs dans un alphabet fini et émises par des sources à
faible dépendance, [116] obtient des
résultats de convergence sur la profondeur d'insertion et sur la
hauteur en supposant que la source est uniformément mélangeante.
La difficulté principale dans l'étude des propriétés asymptotiques des arbres-CGR
provient de la dépendance des mots à insérer et des structures
potentiellement auto-recouvrantes des mots. Les preuves utilisées dans ce travail font appel aux études donnant
des résultats sur la loi des positions d'occurrences d'un mot le long
d'une séquence. [15] déterminent la fonction
génératrice de ces lois dans le cas de suites i.i.d. , à partir d'une relation de récurrence sur les
probabilités. Ce résultat est généralisé par [41] dans le cas d'une séquence Markovienne
d'ordre $1$.
On suppose que le processus des lettres de $m=a_{1}a_{2}\ldots
a_{n}\ldots$ forme une chaîne
de Markov d'ordre $1$ à espace d'états fini $\CA=\{A,C,G,T\}$, irréductible,
apériodique, stationnaire, de matrice de transition $Q$ et de mesure invariante $\pi$.
Pour un mot infini fixée déterministe $s$, on note $s^{(n)}$ le mot
constitué des $n$ premières lettres de $s$, c'est-à-dire $s^{(n)}=s_{1} \dots
s_{n}$, où $s_{i}$ désigne la $i$ème lettre de
$s$. La mesure $\pi$ est étendue aux mots $s^{(n)}$ retournés en posant
$\pi(s^{(n)})\egaldef \pi(a_{1}=s_{n}, \ldots, a_{n}=s_{1})$. On inverse le
mot du fait de la construction de l'arbre-CGR basée sur les préfixes inversés. On définit également les constantes
| $ h_+$ | $\egaldef$ | $\lim_{n\to +\infty}\frac{1}{n}\max\Bigl\{\log\Bigl(\frac{1}{\pi\bigl(s^{(n)}\bigr)}\Bigr)\ \Big| \ \pi\bigl(s^{(n)}\bigr)>0\Bigr\},$(31) |
| $ h_-$ | $\egaldef$ | $\lim_{n\to +\infty}\frac{1}{n}\min\Bigl\{\log\Bigl(\frac{1}{\pi\bigl(s^{(n)}\bigr)}\Bigr)\ \Big| \ \pi\bigl(s^{(n)}\bigr)>0\Bigr\},$(32) |
| $ h$ | $\egaldef$ | $\lim_{n\longrightarrow +\infty}\frac{1}{n}\E\Bigl[\log\Bigl(\frac{1}{\pi\bigl(m^{(n)}\bigr)}\Bigr)\Bigr].$ |
On introduit enfin les variables suivantes:
- $\ell_{n}$, la longueur du plus court chemin de la racine à une feuille de l'arbre $\CT_{n}$;
- $\CL_{n}$, la longueur du chemin le plus long de la racine à une feuille de l'arbre $\CT_{n}$;
- $D_{n}$, la profondeur d'insertion de $m(n)$ dans l'arbre $\CT_{n-1}$ (pour créer $\CT_{n}$);
- $\Delta_{n}$, la longueur d'un chemin de l'arbre $\CT_{n}$, choisi aléatoirement et uniformément parmi les $n$ chemins possibles.
Notons que $\CL_n$ représente la hauteur de
l'arbre. Quant à $\ell_n$, elle donne des renseignements sur le niveau de
saturation. L'analyse de la hauteur et du niveau de saturation est généralement motivée par l'optimisation du coût de mémoire. La hauteur est clairement pertinente de ce point de vue et le niveau de saturation est algorithmiquement pertinent du fait que les nœuds internes en dessous du niveau de saturation sont souvent remplacés par un tableau moins coûteux. Ces paramètres dépendent essentiellement des caractéristiques de la source.
Les variables aléatoires définies ci-dessous jouent un rôle clé dans les preuves. Pour
bien fixer le cadre, on rappelle que $s$ est une donnée déterministe et que
l'aléa n'est engendré que par le mot $m$, c'est-à-dire par la construction
des arbres $\CT_{n}$.
| $X_{n}(s)$ | $\egaldef$ | $ \left \{ \begin{array}{l} 0 \ \text{si}\ s_{1}\ \text{n'est pas dans}\ \CT_{n} \\ \max \{k\geq 1 \ |\ \text{le mot}\ s ^{(k)}\ \text{est déjà inséré dans} \ \CT_{n}\} \end{array} \right. $ |
| $T_{k}(s)$ | $\egaldef$ | $ \min\{n\geq 1\ |\ X_{n}(s)=k\}.$ |
La variable $T_{k}(s)$ admet la décomposition
Quelques éléments de preuve:
La profondeur d'insertion $D_{n}$ est définie comme la longueur du chemin
partant de la racine et conduisant au nœud où $m(n)$ est inséré. En
d'autres termes, $D_{n}$ est le nombre de lettres nécessaires à parcourir
avant de trouver la position de $m(n)$. Le théorème Théorème 4 a des
conséquences immédiates sur le comportement asymptotique de $D_{n}$. En
effet, puisque $D_{n}=\ell_{n}$ lorsque $\ell_{n+1}>\ell_{n}$, ce qui se produit
infiniment souvent presque sûrement puisque $\displaystyle\lim_{n \to \infty} \ell_{n}=\infty$ p.s., on en
déduit que
\[\liminf_{n \to \infty}\frac{D_{n}}{\log n}=\liminf_{n \to
\infty}\frac{\ell_{n}}{\log n}=\frac{1}{h_+}.\]
De même, puisque $D_{n}=\CL_{n}$ lorsque $\CL_{n+1}>\CL_{n}$, on a
\[\limsup_{n \to \infty}\frac{D_{n}}{\log n}=\limsup_{n \to
\infty}\frac{\CL_{n}}{\log n}=\frac{1}{h_-}.\]
La visualisation des répétitions de sous-mots dans l'arbre-CGR suggère un rapprochement avec
l'arbre des suffixes.
Ces arbres ont été introduits par [142]
pour accélérer les opérations de recherche de motifs. Ils se construisent sur le même
schéma récursif que les tries,
à partir de l'ensemble des suffixes d'un mot donné. Dans la section 5.2, on s'intéresse au comportement asymptotique de l'arbre des suffixes construit à partir d'une source VLMC.
Le Trie (abréviation de retrieval) est une structure de données introduite par [52], efficace pour chercher des mots dans un ensemble donné et utilisée dans de nombreux algorithmes de compression de données comme les correcteurs d'orthographe ou les systèmes de recherche d'adresses IP. Le trie utilise une règle de construction récursive qui sépare les mots selon leurs préfixes. On stoppe la procédure dès que tous les mots sont distingués. Un trie est un arbre digital dans lequel les mots sont insérés sur les noeuds externes (les feuilles).
De même que pour les DST, dès qu'un ensemble de mots est donné, la façon dont ils sont insérés dans le trie est déterministe. Néanmoins, un trie devient aléatoire quand les mots sont tirés au hasard par exemple quand chaque mot est produit par une source probabiliste. Un trie des suffixes est un trie construit sur les suffixes de un mot infini. Le hasard vient alors de la source de production d'un tel mot infini et les mots successifs insérés dans l'arbre sont, comme pour l'arbre-CGR, loin d'être indépendants .
Les tries des suffixes, également appelés arbres des suffixes dans la littérature, ont été développés avec les outils de l'analyse d'algorithmes, de la théorie des probabilités et de la théorie ergodique. La construction de ces algorithmes date des travaux de [142] en 1973 et on trouve depuis de nombreuses applications en informatique et en biologie (voir par exemple le livre de [65]). Comme application majeure des tries des suffixes on peut citer le célèbre algorithme de compression LZ77. Les premiers résultats sur la hauteur des tries des suffixes sont dus à [128] et [46]. La recherche d'un mot s'effectue efficacement dans un arbre des suffixes: il suffit de descendre dans la branche correspondant au mot. Si le nœud codant le mot est présent, alors ce mot a déjà été rencontré dans la séquence.
La vitesse à laquelle poussent les tries des suffixes (appelés aussi arbres des préfixes dans le livre de [127]) est étroitement liée aux instants de deuxième occurrence des motifs. On trouve des résultats sur ce sujet dans les travaux traitant d'occurrences de mots, de temps d'attente ou d'instants de renouvellement. Citons à titre d'exemple les travaux de [126] ou [144].
On s'intéresse ici à la hauteur $H_n$ et au niveau de saturation $\ell_n$ d'un trie des suffixes $\CT_n$ contenant les $n$ premiers suffixes d'un mot infini produit par une source générée par la VLMC du peigne.
Les arbres des suffixes que l'on rencontre dans la littérature ont une hauteur et un niveau de saturation à croissance logarithmique du nombre de mots insérés. Lorsque les mots insérés dans les tries sont indépendants (on parle de tries ordinaires par opposition aux tries des suffixes), les résultats de [116] reposent sur deux hypothèses concernant la source qui produit les mots: la source est supposée uniformément mélangeante et la probabilité d'un mot est supposée décroître exponentiellement avec sa longueur. Citons aussi l'analyse générale sur les tries de [37] construits à partir de sources dynamiques.
Pour les tries des suffixes, [129] obtient le même résultat, avec une hypothèse plus faible de mélange (toujours uniforme quand même) et avec la même hypothèse sur la mesure des mots. Néanmoins, [126] indique un résultat sur les préfixes de processus ergodiques suggérant que le niveau de saturation des tries des suffixes ne va pas nécessairement croître de façon logarithmique avec le nombre de mots insérés.
Ces structures digitales ont habituellement dans la littérature une hauteur en $\log n$, $n$ étant le nombre de données stockées. Dans l’article [24], nous présentons deux exemples explicites de tries des suffixes où soit la hauteur soit le niveau de saturation n'est pas logarithmique.
Soit $(y_n)_{n\geqslant 1}$ une suite de mots infinis à droite sur $\{ 0,1\}$. On construit à partir de cette suite un processus de tries $(\CT_n)_{n\geq 1}$ qui est une suite croissante d'arbres binaires construite de la façon suivante. L'arbre $\CT_n$ contient les mots $y_1,\dots ,y_n$ sur ses feuilles. Il est obtenu par une construction séquentielle en insérant successivement les mots $y_n$.
Au début, $\CT_1$ est l'arbre contenant la racine et la feuille $0\dots$ (resp. la feuille $1\dots$) si $y_1$ commence par $0$ (resp. par $1$). Pour $n\geq 2$, étant donné un arbre $\CT_{n-1}$, le mot $y_n$ est inséré de la façon suivante. On descend le long de la branche dont les nœuds codent pour les préfixes successifs de $y_n$; quand la branche s'arrête, si un nœud interne est atteint, alors $y_n$ est inséré dans la feuille libre, sinon on fait pousser la branche en comparant les lettres suivantes jusqu'à ce qu'on puisse les insérer dans des feuilles différentes. Comme on le voit sur la Figure 13, un trie n'est pas un arbre complet et l'insertion d'un mot peut faire grandir une branche de plus d'un niveau. Notez que si le trie contient un mot fini $w$ comme nœud interne, il y a déjà au moins deux mots insérés qui ont pour préfixe $w$. Cela indique pourquoi la seconde occurrence d'un mot est importante dans la croissance d'un trie.
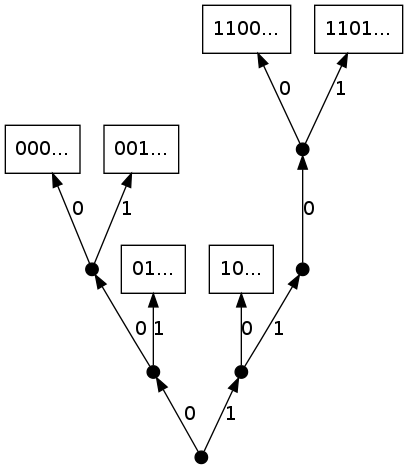$\longrightarrow$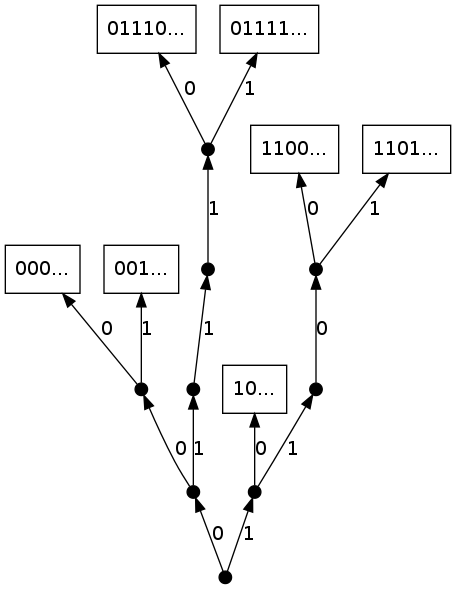 
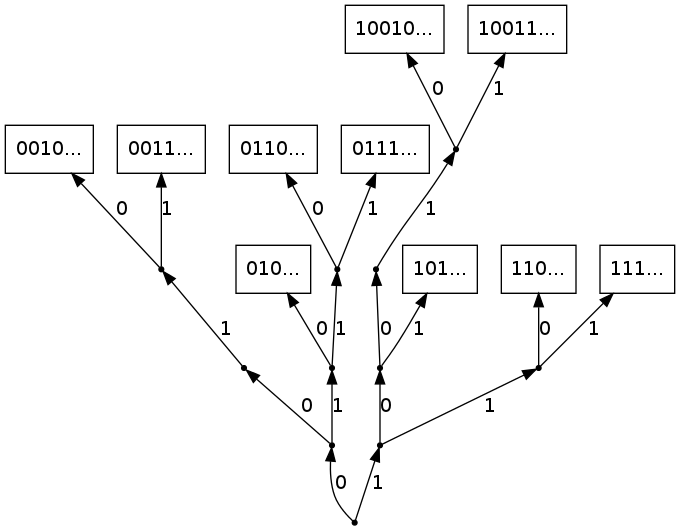
Soit $m\egaldef a_1a_2a_3 \ldots$ un mot infini sur $\{0,1\}$. Le trie des suffixes $\CT_n$ (avec $n$ feuilles) associé à $m$ est le trie construit à partir des $n$ premiers suffixes de $m$ que l'on obtient en effaçant successivement la lettre la plus à gauche, c'est-à-dire
\[
y_1=m,~y_2=a_2a_3a_4\dots, ~y_3=a_3a_4\dots, ~\dots,~y_n=a_na_{n+1}\dots
\]
On note $\CL_n$ la hauteur. On note également $l_n$ le niveau de saturation qui est le niveau maximal auquel tous les nœuds internes sont présents dans $\CT_n$. Formellement, si $\partial \CT_n$ désigne l'ensemble des feuilles de $\CT_n$,
| $ \CL_n$ | $=$ | $\max_{u \in \CT_n\setminus \partial \CT_n} \big\{ |u| \big\}$ |
| $ l_n$ | $=$ | $\max \big\{j \in \Nset | \ \# \{u \in \CT_n\setminus \partial \CT_n, |u|=j\}=2^j\big\}.$ |
Pour le peigne factoriel (voir section 3.3), $\pi(10^n)$ est d'ordre $\frac 1{(n+1)!}$ donc
\[
h_+ \geqslant \lim_{n\to +\infty}\frac{1}{n} \ln\Bigl(\frac{1}{\pi\left(10^{n-1}\right)}\Bigr) = \lim_{n\to +\infty}\frac{\ln n!}{n} = +\infty\]
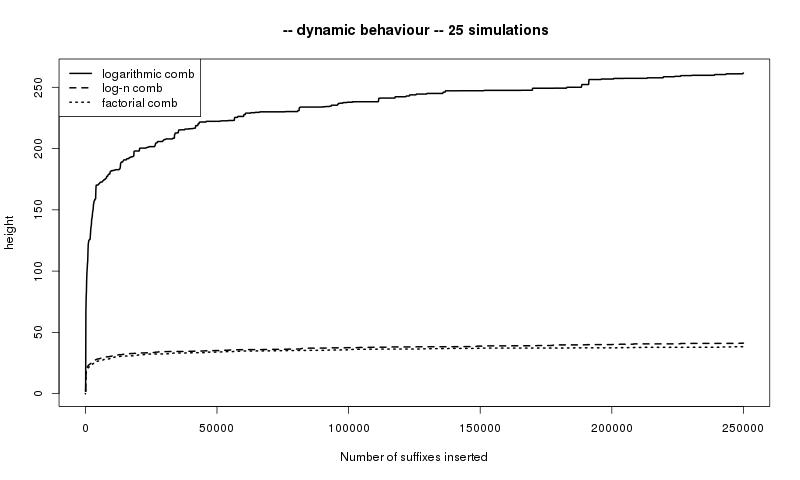
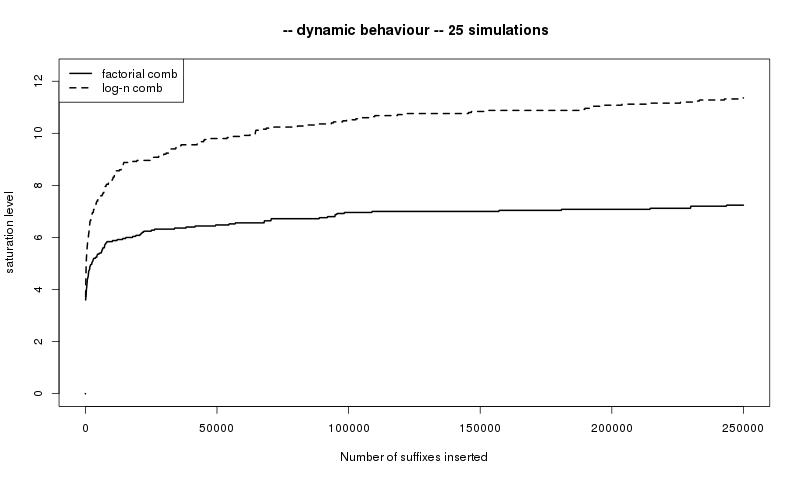
Pour prouver ces deux théorèmes, on utilise la dualité entre les variables $X_n(s)$ et $T_k(s)$, la série génératrice de la deuxième occurrence d'un motif pour une source générée par un peigne, ainsi que les propriétés de mélange de cette même source.
Le comportement dynamique asymptotique de la hauteur et du niveau de saturation des peignes logarithmique et factoriel est représenté sur la Figure 15. Sur les deux graphiques, les courbes en pointillés longs représentent le comportement d'un troisième peigne, appelé peigne en $\ln n$, pour lequel $c_n=\frac13\prod_{k=1}^{n-1}\left(\frac{1}{3}+\frac{1}{(1+k)^2}\right)$ pour $n\geqslant 1$. Ce peigne a un mélange exponentiel, la constante $h_+$ est finie et $h_-$ est strictement positive. La hauteur et le niveau de saturation convergent tous les deux en $\ln n$ (ce résultat est une conséquence des travaux de [116] et [129]).
Ces comportements asymptotiques différents, provenant tous du même modèle, le peigne, illustrent sa richesse.