Perspectives

\( \newcommand\egaldef{\stackrel{\tiny def}{=}} \newcommand{\ep}{\varepsilon} \newcommand{\Zset}{\mathbb{Z}} \newcommand{\Nset}{\mathbb{N}} \newcommand{\Rset}{\mathbb{R}} \newcommand{\Cset}{\mathbb{C}} \newcommand{\CN}{\mathcal{N}} \newcommand{\F}{\mathbb{F}} \newcommand{\E}{\mathbb{E}} \newcommand{\EE}[1]{\E\left[#1\right]} \newcommand{\PCond}[2]{\PP\left[#1\middle| #2\right]} \newcommand{\ECond}[2]{\E\left[#1\middle| #2\right]} \newcommand{\PP}{\mathbb{P}} \newcommand{\CF}{\mathcal{F}} \newcommand{\CG}{\mathcal{G}} \newcommand{\CP}{\mathcal{P}} \newcommand{\CC}{\mathcal{C}} \newcommand{\CD}{\mathcal{D}} \newcommand{\CO}{\mathcal{O}} \newcommand{\CL}{\mathcal{L}} \newcommand{\CA}{\mathcal{A}} \newcommand{\CT}{\mathcal{T}} \newcommand{\CW}{\mathcal{W}} \newcommand{\CS}{\mathcal{S}} \newcommand{\CH}{\mathcal{H}} \newcommand{\CB}{\mathcal{B}} \newcommand{\CM}{\mathcal{M}} \renewcommand{\S}[1]{\ensuremath{S\textsc{\lowercase{#1}}}} \newcommand{\btheta}{\boldsymbol{\theta}} \newcommand{\limite}[2]{\mathop{\longrightarrow} \limits_{\mathrm{#1}}^{\mathrm{#2}}} \newcommand{\limiteloi}[2]{\mathop{\rightsquigarrow} \limits_{\mathrm{#1}}^{\mathrm{#2}}} \newcommand\1{\mathbb{1}} \newcommand\ind[1]{\1_{\{#1\}}} \newcommand\muDisc{\mu_{d}} \newcommand\muDiff{\mu_c} \newcommand{\lpref}{\overleftarrow{\rm pref}} \newcommand{\petitlpref}{\overleftarrow{\rm pref}} \newcommand\idt{\mathbf{I}_H} \newcommand\stp[1]{U_{#1}} \newcommand\ie{\emph{i.e.}} \newcommand\argmin{\mathbf{argmin}} \newcommand\scal[1]{\left\langle #1 \right\rangle} \newcommand\nrm[1]{\left\| #1 \right\|} % \newcommand\abs[1]{\left| #1 \right|} % \DeclareMathOperator{\cv}{\limite{n \to \infty}{}} \DeclareMathOperator{\cvp}{\limite{n \to \infty}{P}} \DeclareMathOperator{\cvl}{\limite{n \to \infty}{\CL}} \DeclareMathOperator{\cvloi}{\limiteloi{n \to \infty}{\CL}} \DeclareMathOperator{\cvmq}{\limite{n \to \infty}{\convLp_2}} \DeclareMathOperator{\trace}{Tr} \newcommand\Rlogo{\protect\includegraphics[height=1.8ex,keepaspectratio]{Rlogo.pdf}} \DeclareMathOperator{\diag}{diag} \DeclareMathOperator{\tr}{tr} \DeclareMathOperator{\dilog}{Li} \DeclareMathOperator{\var}{var} \newcommand\bbox{\hfill\rule{2mm}{2mm}} \newcommand\ordPart[1]{\mathop{\rm \sum _{#1}\uparrow}\nolimits} \DeclareMathOperator{\Hess}{Hess} \newcommand\lUn{L^1} \newcommand\lDeux{L^2} \newcommand\Zbar{\overline{Z}} \newcommand\Tbar{\overline{T}} \newcommand\wass[1]{\mathcal{W}_2\left(#1\right)} \newcommand\law{\mathcal{L}} \newcommand\cstHolder{C_3} \newcommand\cstWass{C_4} \newcommand\cstMoment{C_6} \newcommand\assm[1]{\textbf{A#1}} \newcommand\lmin{\lambda_{min}} \newcommand\cG{c_\gamma} \newcommand\covLimite{\Sigma} \)

$anchor$ Je présente dans ce dernier chapitre un bref panorama de mes perspectives de recherche. Mes projets s'orientent autour de deux thèmes principaux mais non exhaustifs: les chaînes de Markov à mémoire variable et les algorithmes stochastiques.

1. Chaînes de Markov à mémoire variable

1.1. Etude du modèle probabiliste

$anchor$ Le modèle de source VLMC a le mérite d'être suffisamment général pour modéliser de la dépendance non bornée, inclure des processus ne possédant pas de propriétés de renouvellement, tout en permettant de faire des calculs explicites « à la main ». Je souhaite préciser le lien entre l'arbre des contextes probabilisé et la complexité de la source. Qu'est-ce qui résulte de la forme de l'arbre et des lois de probabilités associées aux feuilles ? Quel phénomène sur l'arbre est responsable des propriétés de mélange et du degré de corrélation ? Je souhaite également établir des conditions nécessaires et suffisantes d'existence et d'unicité de mesure invariante pour des arbres plus généraux que le peigne ou le bambou, en évitant les hypothèses classiques et sans doute trop restrictives de non-nullité et continuité:

$\displaystyle\inf_{c \in \CC, \alpha \in /CA}q_c(\alpha)>0$,
l'application $c\mapsto q_c$ est continue.

$anchor$ Si une mesure invariante existe, y a-t-il convergence vers cette mesure et éventuellement à quelle vitesse ? Une première direction de travail est de s'intéresser à un arbre des contextes relativement simple, par exemple un arbre avec un nombre fini de branches infinies quelconques. Sans utiliser le renouvellement comme nous l'avons fait dans les cas du peigne et du bambou, il s'agit de comprendre quels paramètres sur l'arbre des contextes probabilisé influent sur le calcul ou l'existence de la mesure invariante.

$anchor$ Ensuite, on pourra considérer des arbres plus généraux, comme l'arbre possédant toutes les branches codant en base $2$ pour des éléments de $\mathbb{Q}$, avec par conséquent un nombre dénombrable de branches infinies.

$anchor$ Dans les questions relatives à la vitesse de convergence vers l'équilibre, je souhaite pouvoir identifier des conditions garantissant des propriétés de mélange. Dans quels cas a-t-on un mélange uniforme ? Quelle notion de mélange ?

1.2. Applications à la neurobiologie

$anchor$ Dans le cadre d'applications à la neurobiologie avec Bruno Cessac (INRIA Sophia-Antipolis), nous aurions également besoin d'avoir des résultats de type grandes déviations ou des inégalités de concentration non-asymptotique pour adapter les résultats au jeu de données. Généralement, les instants d'émission d'un neurone dépendent de l'activité des neurones sur un voisinage. Ce voisinage est fonction de la configuration des potentiels cumulés. Ce type d'interaction est une « interaction à portée variable ». Ces processus à mémoire (spatiale ou non) variable sont des modèles pertinents dans ce contexte, comme en attestent les travaux de Bruno Cessac [33] et Antonio Galvès et Eva Löcherbach [55]. L'un de nos objectifs est d'utiliser ces modèles pour résoudre des problèmes provenant de la neurobiologie et déterminer les vitesses de convergence pour obtenir un ordre de grandeur sur la taille d'échantillon garantissant une estimation fiable.

1.3. Marches aléatoires persistantes

$anchor$ Nous avons vu dans le chapitre Modélisation de séquences et structures aléatoires discrètes que pour une VLMC $(U_n)_{n\geq 0}$, avec $U_n=\ldots X_{n-1}X_n$, dont l'arbre de contextes possède une branche infinie, le processus des lettres $(X_n)$ n'est en général pas markovien. La marche aléatoire associée aux incréments $(X_n)$

\[ S_t:=\displaystyle\sum_{n=0}^t X_n, \]

$anchor$ pour $t\in\Nset$, est dite persistante et appartient à la famille des processus à mémoire longue. Cette procédure permet d'agrandir la collection des modèles stochastiques utilisés en mathématiques appliquées. Néanmoins, dans de nombreux cas, des modèles en temps continu sont préférés, par exemple en économie et finance. En général, les modèles mathématiques considérés dans ces cadres sont markoviens (mouvement brownien géométrique, processus Cox-Ingersoll-Ross, ...). Par conséquent, ils ne sont pas particulièrement adaptés à la mémoire des agents du marché. Le défi consiste maintenant à utiliser la marche aléatoire associée à des augmentations VLMC afin d'améliorer le cadre continu.

$anchor$ La clé des preuves dans [133] réside dans l'utilisation de propriétés de renouvellement inhérentes aux modèles de type peignes. Il serait intéressant d'étudier des modèles plus généraux: des marches construites à partir d'autres arbres des contextes. Quel est l'impact de la «persistance» dans ce cas plus général ?

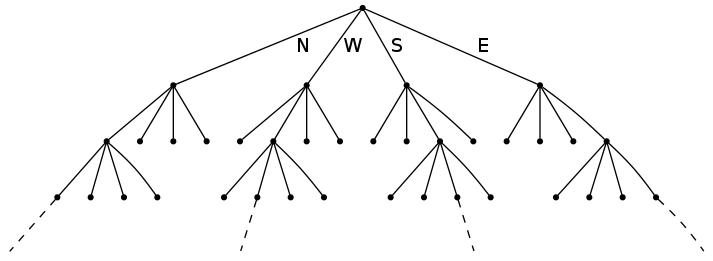
$anchor$ Avec Arnaud Le Ny (LAMA, Université Paris-Est), nous avons commencé à étudier un modèle de marche à mémoire variable en dimension deux, sur le réseau carré $\Zset^2$. Cette marche est construite à partir des incréments à valeurs dans les quatre orientations cardinales $\{N,S,E,W\}$ avec un arbre des contextes dont la forme est donnée sur la Figure 1.

Figure 1:

Arbre de contextes quaternaire associé à la construction d'une marche aléatoire dans le réseau $\Zset^2$.

Y a-t'il un changement de phase, en fonction des lois de probabilités associées à cet arbre de contexte, qui permette de passer d'une chaîne récurrente à une chaîne transiente ?

2. Algorithmes Stochastiques

$anchor$ Les algorithmes stochastiques, en raison de leur caractère récursif, sont particulièrement utiles lorsqu'on observe les données « en ligne ». Ils permettent de faire des estimations avec des procédures, généralement simples, de mise à jour qui ne nécessitent pas la ré-estimation complète du modèle statistique considéré, ré-estimation parfois très coûteuse en temps de calcul. Par ailleurs un grand intérêt de ces approches itératives est qu'elles ne nécessitent pas de stocker en mémoire tous les objets à analyser.

$anchor$ Dans les articles [25, 26], nous avons proposé un algorithme récursif d'estimation de la médiane géométrique, efficace au sens où il se comporte asymptotiquement en loi comme l'estimateur « statique » qui prendrait en compte l'ensemble des observations simultanément. Les résultats théoriques obtenus sur ces algorithmes stochastiques à valeur dans un espace de Hilbert sont tous asymptotiques. Il serait intéressant, en vue d'applications pratiques à des courbes de consommation électrique, d'obtenir des bornes non asymptotiques, à partir d'inégalités de concentration pour des martingales à valeurs dans un espace de Hilbert. L'obtention de bornes qui prennent en compte les différents paramètres du problème permettra de mieux comprendre les performances de l'algorithme à distance finie.

$anchor$ Une autre piste de recherche concerne l'estimation de la matrice, ou l'opérateur pour les espaces fonctionnels, de covariance limite de l'estimateur de la médiane ou de la médiane conditionnelle, à l'aide d'un estimateur récursif correctement pondéré. Il est pour cela nécessaire d'obtenir un résultat de type loi forte quadratique pour des algorithmes stochastiques à valeurs dans un espace de Hilbert. Ceci permettra de calculer des bandes de confiance pour la courbe médiane.

$anchor$ Dans la partie classification non supervisée via l'algorithme séquentiel de type $k$-médianes, il a été prouvé que cet algorithme converge presque sûrement vers un point stationnaire de la fonctionnelle à minimiser. Cependant, l'algorithme peut se retrouver « piégé » par des minima locaux. Il serait intéressant d'obtenir des informations sur la vitesse de convergence et de pouvoir ainsi calibrer les pas de l'algorithme pour contourner ces pièges. Les hypothèses que nous avons utilisées pour établir la convergence ne sont pas facilement vérifiables en pratique et assez techniques. Une méthode analogue à celle utilisée par Pagès [115] pour établir la convergence de l'algorithme de $k$-means à l'aide d'un algorithme de Kohonen pourrait sans doute être une piste intéressante qui permettrait d'obtenir des hypothèses plus élégantes, comme le sont celles de Pagès. De plus, la preuve de la convergence a été établie uniquement en dimension finie et il serait intéressant de la généraliser pour des espaces fonctionnels afin de pouvoir effectuer de la classification de courbes.

3. Vers la biologie ?

$anchor$ Ces pistes de recherche et ces projets sont loin d'être exhaustifs. En particulier, les travaux sur lesquels je me suis penchée depuis ma thèse m'ont éloignée des applications vers la biologie. J'ai toujours été fascinée par la complexité et la beauté du monde vivant et j'ai envie de revenir vers ces problématiques. Ma participation à la Commission Interdisciplinaire 51 du CNRS intitulée « Modélisation et analyse des données et des systèmes biologiques : approches informatiques, mathématiques et physiques » m'a permis de créer des liens avec plusieurs biologistes. J'aimerais réussir à interagir avec eux et m'ouvrir vers de nouvelles thématiques qui me permettront de dégager de nouvelles structures récursives.